Ферментативных реакций кинетика

ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ КИНЕТИКА, изучает закономерности протекания во времени ферментативных р-ций, а также их механизм; раздел кинетики химической.

Каталитич. цикл конверсии в-ва S (субстрата) в продукт P под действием фермента E протекает с образованием промежут. соед. X_i:

где ki - константы скорости отдельных элементарных стадий, K_S - константа равновесия образования фермент-субстратного комплекса X₁ (ES, комплекс Михаэлиса).

При данной т-ре скорость р-ции зависит от концентраций фермента, субстрата и состава среды. Различают стационарную, предстационарную и релаксационную кинетику ферментативных р-ций.

Стационарная кинетика. В стационарном состоянии по промежуточным соед. (dX_i/dt = 0, i = 1, ..., n) и при избытке субстрата , где [S]₀ и [E]₀ - начальные концентрации соотв. субстрата и фермента, кинетика процесса характеризуется постоянным, неизменным во времени уровнем концентраций промежут. соед., а выражение для скорости процесса v₀, наз. начальной стационарной скоростью, имеет вид (ур-ние Михаэлиса- Ментен):

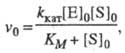(1)

где значения k_кат и К_м - ф-ции констант скорости элементарных стадий и заданы ур-нениями:

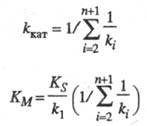
Величину k_кат наз. эффективной каталитич. константой скорости процесса, параметр К_м - константой Михаэлиса. Значение k_кат определяется величинами k_i наиб. медленных стадий каталитич. р-ций и иногда наз. числом оборотов фермента (ферментной системы); k_кат характеризует число каталитич. циклов, совершаемых ферментной системой в единицу времени. Наиб. распространены ферменты, имеющие значение k_кат. для специфич. субстратов в диапазоне 10²-10³ с^-1. Типичные значения константы Михаэлиса лежат в интервале 10^-3- 10^-4 M.

При больших концентрациях субстрата, когда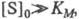 т. е. скорость р-ции не зависит от концентрации субстрата и достигает постоянной величины, наз. макс. скоростью. Графически ур-ние Михаэлиса - Ментен представляет собой гиперболу. Его можно линеаризовать, используя метод двойных обратных величин (метод Лайнуи-вера - Берка), т. е. строя зависимость 1/v от 1/[S]₀, или др. методы. Линейная форма ур-ния (1) имеет вид:

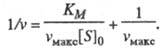(2)

Она позволяет определить графически значения К_м и v_макс (рис. 1).

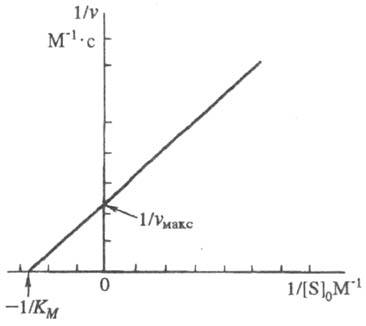
Рис. 1. График линейной трансформации ур-ния Михаэлиса - Ментен в двойных обратных величинах (по Лайнуиверу - Берку).

Величина К_м численно равна концентрации субстрата, при к-рой скорость р-ции равна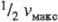 , поэтому К_м часто служит мерой сродства субстрата и фермента, однако это справедливо лишь, если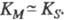

Величины К_м и v_m изменяются в зависимости от значений рН. Это связано со способностью участвующих в катализе групп молекулы фермента изменять свое состояние ионизации и, тем самым, свою каталитич. эффективность. В простейшем случае изменение рН приводит к протонированию или депротонированию, по крайней мере, двух ионизирующихся групп фермента, участвующих в катализе. Если при этом только одна форма фермент-субстратного комплекса (напр., ESH) из трех возможных (ES, ESH и ESH₂) способна превращаться в продукт р-ции, то зависимость скорости от рН описывается ф-лой:

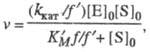
где f = 1 + [H⁺]/K_а + K_b /[H⁺] и f ' = 1 + [H⁺]/К'_а + K'_b/[H⁺] -т. наз. рН-ф-ции Михаэлиса, а К_а, К_b и К'_a, K'_b- константы ионизации групп а и b соотв. своб. фермента и фермент-субстратного комплекса. В координатах lg k_кат - рН эта зависимость представлена на рис. 2, причем тангенсы углов наклона касательных к восходящей, независимой от рН, и нисходящей ветвям кривой должны быть равны соответственно +1, 0 и -1. Из такого графика можно определить значения рК_а групп, участвующих в катализе.

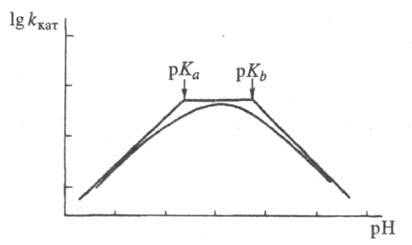
Рис. 2. Зависимость каталитич. константы от рН в логарифмич. координатах.

Скорость ферментативной р-ции не всегда подчиняется ур-нию (1). Один из часто встречающихся случаев - участие в р-ции аллостерич. ферментов (см. Регуляторы ферментов), для к-рых зависимость степени насыщения фермента от [S]₀ имеет негиперболич. характер (рис. 3). Это явление обусловлено кооперативностью связывания субстрата, т.е. когда связывание субстрата на одном из участков макромолекулы фермента увеличивает (положит. кооперативность) или уменьшает (отрицат. кооперативность) сродство к субстрату др. участка.

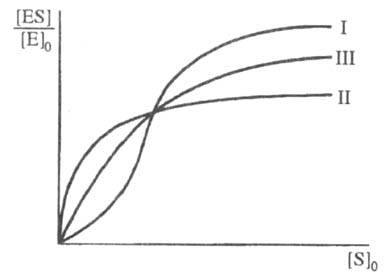
Рис. З Зависимость степени насыщения фермента субстратом от концентрации субстрата при положительной (I) и отрицательной (II) кооперативности, а также в ее отсутствии (III).

Предстационарная кинетика. При быстром смешении р-ров фермента и субстрата в интервале времен 10^-6-10^-1 с можно наблюдать переходные процессы, предшествующие образованию устойчивого стационарного состояния. В этом предстационарном режиме при использовании большого избытка субстрата система дифференц. ур-ний, описывающая кинетику процессов, линейна. Решение данного типа системы линейных дифференц. ур-ний дается суммой экспоненциальных членов. Так, для кинетич. схемы, представленной выше, кинетика накопления продукта имеет вид:

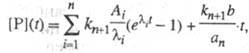
где A_i-, b, а_n - ф-ции элементарных констант скорости; 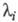-корни соответствующего характеристич. ур-ния.

Величина, обратная 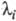, наз. характеристич. временем процесса:

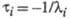
Для р-ции, протекающей с участием n промежут. соед., можно получить n характеристич. времен.

Исследование кинетики ферментативной р-ции в предстационарном режиме позволяет получить представление о детальном механизме каталитич. цикла и определить константы скорости элементарных стадий процесса.

Экспериментально кинетику ферментативной р-ции в предстационарном режиме исследуют с помощью метода остановленной струи (см. Струевые кинетические методы), позволяющего смешивать компоненты р-ции в течение 1 мс.

Релаксационная кинетика. При быстром возмущающем воздействии на систему (изменение т-ры, давления, электрич. поля) время, к-рое необходимо системе для достижения нового равновесия или стационарного состояния, зависит от скорости процессов, определяющих каталитич. ферментативный цикл.

Система ур-ний, описывающая кинетику процесса, линейна, если смещение от положения равновесия невелико. Решение системы приводит к зависимостям концентраций компонентов разл. стадий процесса в виде суммы экспоненциальных членов, показатели экспонент к-рых имеют характер времен релаксаций. Результатом исследования является спектр времен релаксации, соответствующий числу промежут. соед., участвующих в процессе. Величины времен релаксаций зависят от констант скорости элементарных стадий процессов.

Релаксационные методы кинетики позволяют определить константы скорости отдельных элементарных стадий трансформации интермедиатов. Методы изучения релаксационной кинетики имеют разл. разрешающую способность: поглощение ультразвука - 10^-6-10^-10 с, температурный скачок - 1O^-4-10^-6 с, метод электрич. импульса - 10^-4-10^-6 с, скачок давления - 10^-2 с. При исследовании кинетики ферментативных р-ций наиб, применение нашел метод температурного скачка.

Макрокинетика ферментативных процессов. Развитие методов получения гетерогенных катализаторов путем иммобилизации ферментов на разл. носителях (см. Иммобилизованные ферменты)обусловило необходимость анализа кинетики процессов с учетом массопереноса субстрата. Теоретически и экспериментально исследованы закономерности кинетики р-ций с учетом эффектов диффузионного слоя и для систем с внутридиффузионными затруднениями при распределении фермента внутри носителя.

В условиях, когда на кинетику процесса влияет диффузионный перенос субстрата, каталитич. эффективность системы уменьшается. Фактор эффективности 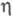равен отношению плотности потока продукта в условиях протекания ферментативной р-ции с диффузионно пониженной концентрацией субстрата к потоку, к-рый мог бы реализоваться в отсутствие диффузионных ограничений. В чисто диффузионной области, когда скорость процесса определяется массопереносом субстрата, фактор эффективности для систем с внешнедиффузи-онным торможением обратно пропорционален диффузионному модулю :

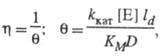
где l_d - толщина диффузионного слоя, D - коэф. диффузии субстрата.

Для систем с внутридиффузионным торможением в р-циях первого порядка

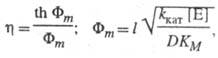
где Ф_т - безразмерный модуль (модуль Тиле).

При анализе кинетич. закономерностей в ферментативных реакторах широкое теоретич. и эксперим. развитие получили "идеальные" модели реакторов, проточный безградиентный реактор (проточный реактор идеального перемешивания), проточный реактор с идеальным вытеснением, мембранный реактор.

Кинетика полиферментных процессов. В организме (клетке) ферменты действуют не изолированно, а катализируют цепи трансформации молекул. Р-ции в полиферментных системах с кинетич. точки зрения можно рассматривать как последоват. процессы, специфич. особенностью к-рых является катализ ферментами каждой из стадий:

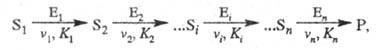
где v_i, K_i - соотв. макс, скорость процесса и константа Михаэлиса i-й стадии р-ции соответственно.

Важная особенность процесса - возможность образования устойчивого стационарного состояния. Условием-его возникновения может служить неравенство v_i > v₀, где v₀ - скорость лимитирующей стадии, характеризуемой наименьшей константой скорости и тем самым определяющей скорость всего последоват. процесса. В стационарном состоянии концентрации метаболитов после лимитирующей стадии меньше константы Михаэлиса соответствующего фермента.

Специфич. группу полиферментных систем составляют системы, осуществляющие окислит.-восстановит. р-ции с участием белковых переносчиков электронов. Переносчики образуют специфич. структуры, комплексы с детерминированной последовательностью переноса электрона. Кинетич. описание такого рода систем рассматривает в качестве независимой переменной состояния цепей с разл. степенью заселенности электронами.

Применение. Ферментативных реакций кинетику широко используют в исследовательской практике для изучения механизмов действия ферментов и ферментных систем. Практически значимая область науки о ферментах - инженерная энзимология, оперирует понятиями ферментативных реакций кинетики для оптимизации биотехнол. процессов.

Лит.: Полторак О. M., Чухрай E. С, Физико-химические основы ферментативного катализа, M., 1971; Березин И.В., Мартинек К, Основы физической химии ферментативного катализа, M., 1977; Варфоломеев С. Д., Зайцев С. В., Кинетические методы в биохимических исследованиях, M.. 1982. С. Д. Варфоломеев.

• Кинетика ферментативных реакций - Наглядная биохимия
• Кинетика ферментативных реакций - Биологическая химия