1.4.3. Методы, основанные на определении формы неподвижных капель и пузырьков
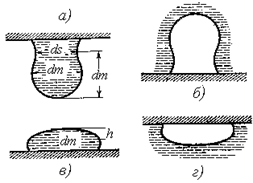
Под действием поверхностного натяжения маленькие капли и пузырьки стремятся принять сферическую форму. Если каплю жидкости поместить в среду той же плотности, то эта капля обязательно примет сферическую форму. Если же плотность капли (или пузырька газа) будет отличаться от плотности среды, то действие поверхностного натяжения будет соизмеримо с действием гравитационных сил и капля (или пузырек) будет иметь форму не сферы, а некоторой фигуры вращения, например, показанной на рис. 1.8. По форме этих капель (или пузырьков газа) с применением уравнения Лапласа можно рассчитать поверхностное натяжения жидкости. Для этого определяют такие параметры капель или пузырьков, которые характеризуют отклонение формы капель (или пузырьков) от сферической.
Метод висящей капли.Висящая капля (или пузырек) вытягивается по мере роста до тех пор, пока гидростатическое давление не уравновесится давлением, обусловленным кривизной поверхности. Для определения поверхностного натяжения по форме таких пузырьков и капель измеряют S = ds/dm, где dm – максимальный диаметр капли (пузырька); ds – диаметр, измеренный на расстоянии dm от нижней точки капли (или верхней точки пузырька). Расчет поверхностного натяжения проводят по формуле
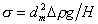 , (1.1.63)
, (1.1.63)
где Dr – разность плотностей исследуемой жидкости (капли) и окружающей ее среды (газ) или пузырька и жидкости, в которой он формируется; H – безразмерный параметр, который приводится в таблицах Бешфорта, Адамса и Штауфера в зависимости от параметра S.
По изменению формы висящей капли во времени можно определить зависимость поверхностного натяжения от времени и охарактеризовать кинетику формирования адсорбционного слоя поверхностно-активных веществ.
Метод лежащей капли или сидящего пузырька.Как видно из рис. 1.8, лежащая капля и сидящий пузырек симметричны. Поэтому рассмотрим определение поверхностного натяжения на примере капли.
Для крупных капель расчет ведут по уравнению
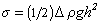 , (1. 1.64)
, (1. 1.64)
где h – расстояние от вершины капли до ее максимального сечения.
Для мелких капель необходимо определять их параметры: h – расстояние от максимального сечения до вершины капли; dm – ее максимальный диаметр. Затем по таблицам Бешфорта – Адамса находят f (b) при измеренном значении dm и рассчитывают
поверхностное натяжение по формуле
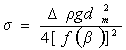 . (1.1.65)
. (1.1.65)
Рис. 1.8. Формы сидящих и висящих капель и пузырьков: а - висящая капля, б - висящий пузырек, в - сидящая капля, г - сидящий пузырек |
Экспериментальные приборы измерения поверхностного натяжения по этому методу включают аппаратуру для получения симметричной капли, обеспечения чистоты поверхности раздела фаз, предотвращения испарения с поверхности, поддержания и контроля параметров состояния и непосредственного измерения размеров капли или для ее фотографирования и определения размеров на фотоснимке. Вследствие того, что поверхностное натяжение зависит от природы контактирующих фаз, а для установления равновесия требуется определенное, подчас значительное, время, более точные результаты получаются при фотографировании капель. Для обеспечения погрешности не более 1-2% при измерении поверхностного натяжения на границе жидкость - пар и 2-4% на границе жидкость-жидкость необходимо обеспечить измерение капель или пузырьков с погрешностью, не превышающей 0,1%.
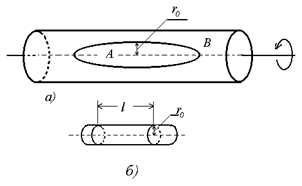
Рис. 1.9. Схема вращающегося капилляра с каплей жидкости (а) и капля жидкости (б) |
Основными достоинствами методов, основанных на измерении размеров пузырьков или капель, являются независимость найденного поверхностного натяжения от краевых углов смачивания, возможность изучения границ раздела жидкость-газ и жидкость-жидкость независимо от их вязкости при высоких давлениях и температуре, при значительном изменении времени существования поверхности (от 10 с до нескольких часов). К недостаткам указанных методов можно отнести длительность единичного измерения поверхностного натяжения и сложность устройств, предотвращающих испарение с поверхности жидкость-газ, и необходимость предварительного изучения распределения компонентов в системе двух жидкостей для изучения явлений переноса массы через межфазную границу. Как разновидность метода неподвижной капли можно рассматривать метод вращающейся капли одной жидкости в среде другой жидкости. Этот метод очень удобен для измерения предельно низкого межфазного натяжения на границе жидкость - жидкость и позволяет измерить необычно низкое межфазное натяжение (до 10-3 мДж/м2) с высокой точностью.
Экспериментальная установка включает блок, обеспечивающий вращение с постоянной скоростью капилляра, в который помещают жидкость В (воду или исследуемый раствор) и каплю другой жидкости А (углеводород) (рис. 1.9). Если плотность жидкости А меньше плотности жидкости В, то капля при вращении располагается в центре капилляра. По мере увеличения частоты вращения происходит вытягивание капли, так как центробежная сила противодействует поверхностному натяжению. При достаточно большой частоте вращения капля принимает форму вытянутого цилиндра. Рассмотрение общей энергии цилиндра длиной l и радиуса r0, включающей в себя потенциальную энергию и свободную поверхностную энергию, приводит к уравнению
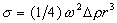 , (1.1.66)
, (1.1.66)
где w- частота вращения, Dr - разность плотностей жидкостей.
Уравнение (1.1.66), известное как уравнение Воннегута, справедливо для цилиндрических вращающихся капель.
Расчет поверхностного натяжения эллиптических капель проводится по более сложному уравнению. Поэтому стремятся подобрать частоту вращения таким образом, чтобы капля приобрела цилиндрическую форму. Хотя этот метод позволяет точно измерять небольшое межфазовое натяжение, его применение сдерживается сложностью экспериментальных установок.