5.2.Адсорбция ионов на заряженной поверхности, несущей двойной ионный слой

В предыдущем разделе мы рассмотрели основные закономерности процесса адсорбции из растворов неионизированных веществ на незаряженной поверхности.

Исследования адсорбции из растворов на заряженной поверхности ионизированных молекул, например, красителей и поверхностно-активных веществ, относятся к той области коллоидной науки, которая в настоящее время очень активно развивается, особеннов той части, котораякасается выбора модели для их количественной обработки. Часто адсорбцию в таких системах рассматривают как ионообменный процесс, по крайней мере, на начальной стадии, т.е. при малых степенях заполнения адсорбционного слоя :

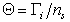, (1.5.12)

где Г_i– адсорбция i-того компонента (моль/м²); n_s– число активных мест на единице площади поверхности (моль/м²). Однако, оказалось, что из-за сильного специфического взаимодействия органическихионов с поверхностью адсорбента и зависимости электростатического взаимодействия от степени их необратимого связывания в двойном слое, а также из-за резкого усиления при этом латеральных взаимодействий между адсорбированными частицами (отклонения коэффициента активности от единицы) по мере заполнения адсорбционного слоя обычные уравнения ионного обмена (изотермы Доннана, Никольского, Ленгмюра) неприменимы для относительно крупных, содержащих 10-12 атомов углерода, органических ионов. Адсорбцию таких веществ следует рассматривать как особый случай специфической адсорбции.

Более строгое количественное описание специфической адсорбции органических ионов для малых степеней заполнения поверхности адсорбента позволяют получить подходы Штерна - Ленгмюра и Штерна -Грэма.

При выводе изотермы адсорбции (Штерна - Ленгмюра) ионизированных частиц на заряженной поверхности обычно делаются следующие предпосылки.

1. Специфически адсорбируется только один вид ионов (в нашем случае ионы ПАВ или красителя). Поэтому плотность (r) заряда, образующегося во внутреннем слое Гельмгольца

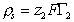, (1.5.13)

где индекс 2 относится к иону (ПАВ, красителя или другого органического иона с большим углеводородным радикалом).

Это допущение реализуется лишь в области разбавленных растворов.

2. Собственный размер адсорбированного иона считается таким, что ион занимает лишь активный центр, по величине соизмеримый с молекулой растворителя (воды), которая при этом вытесняется. Если это относить к иону ПАВ, то следует считать, что адсорбция происходит с ориентированием углеводородного радикала нормально к поверхности.

3. Поверхность адсорбента считается однородной, и допускается возможность учета электрических взаимодействий через среднее значение потенциала. Строго говоря, эта предпосылка вносит известное противоречие в подход к рассмотрению механизма данного процесса, так как, с одной стороны, в соответствии с п.2 адсорбцию следует рассматривать как локализованную на дискретных активных адсорбционных центрах, а с другой – используется понятие усредненного – «размазанного» – потенциала адсорбционного поля 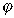. Иначе говоря, используется приближение Брэгга - Вильямса, которое применяется в термодинамике, чтобы сохранить возможность разделения суммы по состояниям в неидеальных системах.

4. При выводе уравнения Штерна не учитываются дипольные взаимодействия, изменения параметров собственной ионной атмосферыадсорбированных ионов ПАВ и латеральные взаимодействия цепь-цепь. Эта предпосылка в какой-то мере может соблюдаться лишь в области бесконечно разбавленных адсорбционных слоев, т.е. при низких степенях заполнения поверхности ионами ПАВ (или красителей). Уравнение Штерна выводится аналогично приведенному выше выводу уравнения Ленгмюра и имеет вид

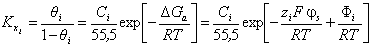,(1.5.14)

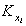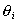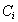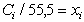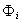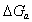где – постоянная равновесия процесса адсорбции; - степень заполнения поверхности адсорбента при адсорбции i-того сорта ионов (ПАВ, красителей); – равновесная концентрация (моль/л), - молярная доля растворенного вещества; z_i- заряд данного иона (с учетом знака); - специфический адсорбционный потенциал (свободная энергия специфической адсорбции); - потенциал в адсорбционном поверхностном слое; -cвободная энергия адсорбции, зависящая от специфического потенциала 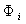и потенциала в плоскости адсорбции.

Уравнение (1.5.14), учитывающее адсорбцию только одноготипа ионов, является упрощенным вариантом более сложного уравнения, выведенного Штерном, в котором рассматривается специфическая адсорбция двух типов ионов.

При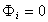 уравнение (1.5.14) переходит в уравнение Ленгмюра, в котором энергия адсорбции равна 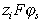; поэтому его можно рассматривать как аналог уравнения Ленгмюра, «исправленного» для специфической адсорбции.

Учет собственного размера молекул (площади, занимаемой адсорбированными молекулами) приводит к уравнению Фольмера:

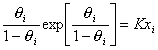. (1.5.15)

Уравнение (1.5.15) отличается от уравнения (1.5.14) экспоненциальным членом 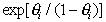, который при низких значениях 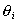не оказывает существенного влияния на ход изотермы, но при высоких 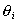его влияние сказывается в менее интенсивном приближении изотермы к насыщению.

При низких степенях заполнения адсорбционного слоя, 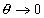, может быть использовано уравнение, предложенное Грэмом (подход Штерна-Грэма):

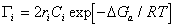, (1.5.16)

где 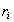– радиус проекции адсорбированного иона.

Уравнение (1.5.16) является аналогом уравнения Генри. При интерпретации экспериментальных данных в области малых степеней заполнения адсорбента с помощью уравнения (1.5.16) допускается проявление латеральных взаимодействий между гидрофобными частями адсорбированных ионов, что позволяет на полуколичественном уровне провести анализ сложных адсорбционных процессов.

Латеральные взаимодействия при формировании адсорбционного слоя учитываются и в уравнении Фрумкина-Фаулера-Гуггенгейма (ФФГ), которое имеет вид

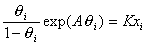, (1.5.17)

где постоянная 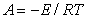, учитывающая энергию латерального взаимодействия Е, определяется из максимального угла наклона изотермы 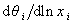при 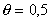. При выводе уравнения (1.5.17) предполагалось, что постоянная А является независимой от степени заполнения адсорбционного слоя. В действительности это соблюдается далеко не всегда. При низких степенях заполнения эта постоянная отражает электростатическое отталкивание адсорбированных ионов, а при высоких - притяжение их углеводородных частей. В этой связи постоянная А при насыщении монослоя может не только изменяться по величине, но и менять знак. Поэтому применение изотермы (ФФГ) может быть полезным лишь для оценки изменения электростатического взаимодействия в зависимости от степени заполнения поверхности адсорбента в области разбавленных адсорбционных слоев.