5.3. Энергия Гиббса и механизм адсорбции из растворов на твердой поверхности5.3.1. Молекулярная адсорбция
В этом разделе рассмотрим закономерности определения энергии Гиббса адсорбции неионогенных веществ из водных растворов и адсорбции из неводных растворов. Растворы ПАВ с начальной концентрацией выше ККМ содержат мицеллы. В этой связи механизм адсорбции, молекулярный или мицеллярный, можно выявить по соотношению энергий Гиббса процессов мицеллообразования и адсорбции. Энергия Гиббса процесса адсорбции рассчитывается по уравнению
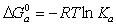 , (1.5.18)
, (1.5.18)
где Kа– постоянная адсорбционного равновесия, учитывающая обменный характер адсорбции из растворов. Эта постоянная определяется по начальному участку изотермы адсорбции при формировании ненасыщенного адсорбционного слоя.
Адсорбционный молекулярный слой, формируемый при адсорбции из растворов, можно рассматривать как двумерную фазу, в которой отношение компонентов определяется различиями в энергии взаимодействия их молекул с активными центрами поверхности адсорбента, а суммарное относительное заполнение поверхности всегда равно единице, т.е. для двухкомпонентного раствора в расчете на единицу массы адсорбента
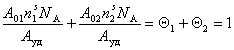 , (1.5.19)
, (1.5.19)
где  – площадь, занятая молекулой растворителя и растворенного вещества в адсорбционном слое;
– площадь, занятая молекулой растворителя и растворенного вещества в адсорбционном слое; 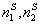 – число молей адсорбированных растворителя и растворенноговещества; Aуд– удельная поверхность адсорбента;
– число молей адсорбированных растворителя и растворенноговещества; Aуд– удельная поверхность адсорбента;  -число Авогадро;
-число Авогадро; 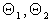 - доля поверхности, занятая молекулами растворителя и ПАВ, соответственно.
- доля поверхности, занятая молекулами растворителя и ПАВ, соответственно.
Уравнение (1.5.19) справедливо для непористых и крупнопористых адсорбентов при обратимой адсорбции. Выражая концентрации компонентов в адсорбционном слое в мольных долях, получаем для парциальной постоянной равновесия каждого компонента, например, для ПАВ,
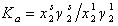 , (1.5.20)
, (1.5.20)
где 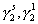 – коэффициенты активности ПАВ в адсорбционном слое и в растворе.
– коэффициенты активности ПАВ в адсорбционном слое и в растворе.
Учитывая соотношение 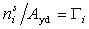 , можем записать уравнение (1.5.19) как
, можем записать уравнение (1.5.19) как
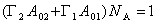 . (1.5.21)
. (1.5.21)
Пренебрегая адсорбцией растворителя, т.е. полагая, что Гm1 = 0, и учитывая выражение 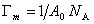 , можем написать для начального участка изотермы адсорбции уравнение
, можем написать для начального участка изотермы адсорбции уравнение
 . (1.5.22)
. (1.5.22)
Тогда мольные доли адсорбированных веществ можно выразить как
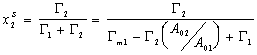 (1.5.23)
(1.5.23)
и
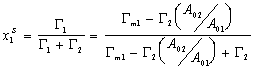 . (1.5.24)
. (1.5.24)
Можно считать, что
 , (1.5.25)
, (1.5.25)
где 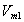 – мольный объем растворителя.
– мольный объем растворителя.
Мольные доли компонентов в растворе рассчитываются обычным путем.
Коэффициенты активности стремятся к единице при бесконечном разбавлении, поэтому для нахождения постоянной адсорбционного равновесия экспериментальные данные экстраполируют к 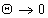 . Такая экстраполяция выполняется в координатах
. Такая экстраполяция выполняется в координатах 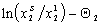 .
.
Пример изотермы адсорбции поверхностно-активного вещества - диэтилгексадецилбензолсульфоната натрия на хлопке - из неводного раствора (растворитель - перхлорэтилен) приведен на рис. 1.46. Эта изотерма может быть отнесена к типу L-4. В данном случае формирование как первого, так и последующих слоев происходит при равновесной концентрации, во много раз меньшей, чем ККМ.
|
На рис. 1.47 показаны эти же экспериментальные данные для начального участка изотермы, обработанные в координатах экстраполяции для нахождения состава адсорбционного слоя. Постоянную равновесия адсорбции можно рассчитать как 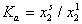 . Для этого строится изотерма в координатах
. Для этого строится изотерма в координатах 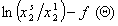 .
.
Предполагается, что растворитель не адсорбируется и тогда найденные значения постоянной адсорбционного равновесия при 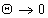 позволяют рассчитать изменение энергии Гиббса при адсорбции. Для такого случая адсорбции она составляет величину в несколько десятков кДж/моль, в то время как энергия Гиббса мицеллообразования этого ПАВ при той же температуре составляет несколько кДж/моль.
позволяют рассчитать изменение энергии Гиббса при адсорбции. Для такого случая адсорбции она составляет величину в несколько десятков кДж/моль, в то время как энергия Гиббса мицеллообразования этого ПАВ при той же температуре составляет несколько кДж/моль.
|
Становится очевидным, что адсорбция таких веществ на твердой поверхности будет подавлять мицеллообразование и протекать по молекулярному механизму. Отметим, что для построения графика в координатах (рис. 1.47) необходимо независимо измерять как равновесную адсорбцию, так и количество адсорбированного вещества. Такую возможность дает метод радиоактивной метки на адсорбируемом веществе.
Адсорбция на мелкопористом адсорбентеЧасто переход от мономолекулярной адсорбции к полимолекулярной из водных растворов ПАВ на неполярных непористых адсорбентах и на полярных непористых адсорбентах из среды органических растворителей с малой диэлектрической проницаемостью происходит в области равновесных концентраций, близких ККМ.
|
Агрегированные слои образуются и при адсорбции поверхностно-активных веществ на полярном мелкопористом адсорбенте. Пример такой изотермы адсорбции приведен на рис. 1.48. Перегиб на изотермах, соответствующий завершению формирования первого монослоя в таких системах наблюдается при ККМ в равновесных растворах. Это происходит потому, что энергия Гиббса адсорбции и мицеллообразования имеют один порядок, что является основным отличием адсорбции ПАВ на мелкопористых сорбентах, поры которых недоступны для адсорбата, по сравнению с волокнами, адсорбция на которых может сопровождаться диффузией ПАВ внутрь. Вместе с тем можно полагать, что адсорбция на мелкопористых адсорбентах протекает с агрегированием адсорбционного слоя, по-видимому, с образованием надмолекулярных структур с пониженной подвижностью молекул ПАВ.
Адсорбция на крупнопористых адсорбентах
|
Несколько иной характер адсорбции наблюдается для крупнопористых адсорбентов, когда адсорбируются оба компонента раствора. В таких системах равновесие наступает при концентрациях выше ККМ. Зависимость гиббсовской адсорбции в них проходит через максимум. Пример такой зависимости приведен на рис. 1.49. Во избежание неправильной интерпретации изотермы адсорбции следует учитывать и адсорбцию растворителя, в связи с чем для обработки экспериментальных данных следует использовать уравнение Эверетта (1.5.8). В таких системах адсорбцию можно рассчитывать как отнесенную к массе адсорбента, так и к его удельной поверхности, найденной независимым методом, например, по адсорбции азота.
Рис. 1.50. Изотерма адсорбции в координатах уравнения Эверетта |
Как пример на рис. 1.50 приведена изотерма адсорбции диэтилдодецилбензолсульфоната на силикагеле в линейной форме уравнения Эверетта. Такая зависимость позволяет определить предел адсорбции и постоянную обмена K. Следует отметить, что построение зависимостей в координатах уравнения Эверетта (1.5.8) требует кропотливой работы по независимому определению количества адсорбированного вещества непосредственно на поверхности адсорбента и определения состава равновесного раствора. Это позволяет рассчитать состав адсорбционного слоя. Затем по найденным значениям постоянной равновесия адсорбции Kа и предела адсорбции рассчитывается изотерма адсорбции с использованием уравнения Ленгмюра в форме (1.5.11). Пример полученных данных представлен на рис. 1.51. Полученная изотерма адсорбции носит типичный для ленгмюровских кривых вид с насыщением мономолекулярного слоя при концентрациях, близких ККМ, причем молекулярные площадки свидетельствуют о расположении молекул адсорбата на поверхности адсорбента «плашмя», т.е. при взаимодействии с поверхностью как полярных групп, так и углеводородных радикалов.
|
Расчет энергии Гиббса адсорбции на крупнопористом адсорбенте проводят следующим образом.
Общий объем адсорбционного слоя можно представить в виде суммы парциальных объемов адсорбированных компонентов.
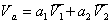 , (1.5.26)
, (1.5.26)
где 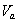 - объем мезопор адсорбента, найденный по низкотемпературной адсорбции азота;
- объем мезопор адсорбента, найденный по низкотемпературной адсорбции азота; 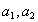 – величины удельной адсорбции растворителя и ПАВ в расчете на единицу массы адсорбента;
– величины удельной адсорбции растворителя и ПАВ в расчете на единицу массы адсорбента; 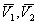 – мольные объемы растворителя и ПАВ. Мольная доля ПАВ в общем количестве адсорбированных компонентов равна
– мольные объемы растворителя и ПАВ. Мольная доля ПАВ в общем количестве адсорбированных компонентов равна
 . (1.5.27)
. (1.5.27)
Выразив  из уравнения (1.5.26) и подставив в уравнение (1.5.27), получаем
из уравнения (1.5.26) и подставив в уравнение (1.5.27), получаем
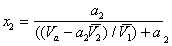 . (1.5.28)
. (1.5.28)
Экстраполяция экспериментальных данных к 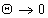 выполняется в тех же координатах, что и при адсорбции на волокнах. Рассчитанные значения энергии Гиббса адсорбции показывают, что увеличение длины углеводородного радикала ПАВ затрудняет адсорбцию на пористом адсорбенте.
выполняется в тех же координатах, что и при адсорбции на волокнах. Рассчитанные значения энергии Гиббса адсорбции показывают, что увеличение длины углеводородного радикала ПАВ затрудняет адсорбцию на пористом адсорбенте.
Таким образом, характер адсорбции зависит как от природы ПАВ, так и от вида адсорбента. Характер адсорбции во многом определяет такие процессы, как поверхностное модифицирование волокон- например, антиэлектростатическую обработку, моющее действие ПАВ и т.д.
Адсорбция ионов из водных растворов на заряженной поверхности
При изучении адсорбции из водных растворов, например красителей на поверхности волокон, в качестве характеристики их сродства к адсорбенту часто используют изменение энергии Гиббса в процессе перехода из раствора на поверхность по постоянной адсорбционного равновесия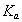 (1.5.18), заменяя активность на концентрацию и определяя количество адсорбированного вещества по разности концентраций исходного и равновесного растворов.
(1.5.18), заменяя активность на концентрацию и определяя количество адсорбированного вещества по разности концентраций исходного и равновесного растворов.
Хотя эта характеристика, рассчитанная по уравнению (1.5.18), используется достаточно широко в технической литературе и в ряде учебников по технологии текстильных производств, применение ее встречает, по крайней мере, два затруднения, которые чаще всего делают найденные величины неопределенными.
Во-первых, расчет 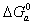 по уравнению (1.5.18) предполагает, что как раствор, так и адсорбционный слой должны быть бесконечно разбавленными с тем, чтобы избежать введения коэффициентов активности при замене активностей на концентрации, причем в обязательном порядке выраженные через молярные доли
по уравнению (1.5.18) предполагает, что как раствор, так и адсорбционный слой должны быть бесконечно разбавленными с тем, чтобы избежать введения коэффициентов активности при замене активностей на концентрации, причем в обязательном порядке выраженные через молярные доли 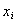 в обеих равновесных частях системы, а это означает, что требуется определять состав адсорбционного слоя.
в обеих равновесных частях системы, а это означает, что требуется определять состав адсорбционного слоя.
Во-вторых, уравнение (1.5.18) предполагает, что между молекулами адсорбата (красителя, ТВВ) и субстратом (волокном) проявляются лишь силы межмолекулярного взаимодействия ван-дер-ваальсова типа (а также молекулярные или даже химические взаимодействия) в отсутствие электрических сил. Но поскольку мы рассматриваем адсорбцию на заряженной поверхности (а все без исключения волокна в водной среде несут на своей поверхности двойной ионный слой), в расчетах сродства необходимо учитывать изменение электрохимического потенциала
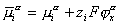 , (1.5.29)
, (1.5.29)
который определяется как сумма работ переноса моля частиц i-того сорта из вакуума в фазу 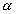 и разделяется на химический потенциал
и разделяется на химический потенциал 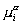 и электростатическую работу
и электростатическую работу  , где zi – заряд частиц с учетом знака, F – число Фарадея,
, где zi – заряд частиц с учетом знака, F – число Фарадея, 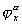 – потенциал (Гальвани) в точкех, в которую помещают данную частицу.
– потенциал (Гальвани) в точкех, в которую помещают данную частицу.
Становится очевидным, что так как потенциал двойного слоя волокон 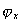 зависит от условий существования системы (температуры, рН среды, наличия индифферентных и неиндифферентных электролитов в растворе совместно с красителем или ПАВ), то и найденные значения
зависит от условий существования системы (температуры, рН среды, наличия индифферентных и неиндифферентных электролитов в растворе совместно с красителем или ПАВ), то и найденные значения 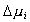 могут быть строгими только при условии, что они определены в точке нулевого заряда волокон, когда
могут быть строгими только при условии, что они определены в точке нулевого заряда волокон, когда 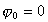 . Даже в изоэлектрической точке, т.е. при
. Даже в изоэлектрической точке, т.е. при 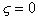 (но
(но  ), найденные значения
), найденные значения 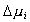 будут все равно иметь погрешность.
будут все равно иметь погрешность.
Рассмотрим влияние двойного слоя на адсорбцию заряженных молекул и покажем возможные пути управления этим процессом, а также способы разделения изменения энергии Гиббса процесса адсорбции 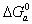 на компоненты с вычленением искомой молекулярной или химической компоненты, что основано на предпосылке аддитивности, т.е.
на компоненты с вычленением искомой молекулярной или химической компоненты, что основано на предпосылке аддитивности, т.е.
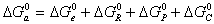 , (1.5.30)
, (1.5.30)
где индексы e, R, P, C обозначают электростатическую компоненту, вклад гидрофобных радикалов, вклад полярных частей и вклад химического взаимодействия в изменении энергии Гиббса при адсорбции.
Обозначим 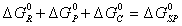 .
.
Величина 
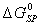 включает вклады всех видов взаимодействия, зависящих от «специфической» (неэлектростатической) природы системы.
включает вклады всех видов взаимодействия, зависящих от «специфической» (неэлектростатической) природы системы.

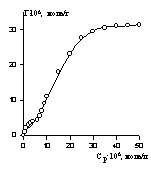 Рис. 1.46. Изотерма адсорбции ПАВ на хлопке из ПХЭ
Рис. 1.46. Изотерма адсорбции ПАВ на хлопке из ПХЭ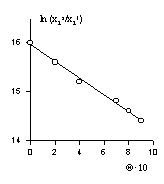 Рис. 1.47. Линейная изотерма адсорбции для определения постоянной равновесия.
Рис. 1.47. Линейная изотерма адсорбции для определения постоянной равновесия.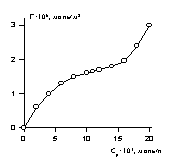 Рис. 1.48. Изотерма адсорбции ПАВ (циклимида) на аэросиле из СCl4
Рис. 1.48. Изотерма адсорбции ПАВ (циклимида) на аэросиле из СCl4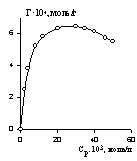 Рис.1.49. Гиббсовская адсорбция ПАВ на
Рис.1.49. Гиббсовская адсорбция ПАВ на 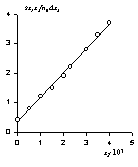
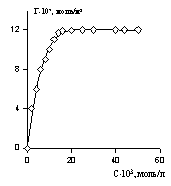 Рис. 1.51. Изотерма адсорбции растворенного вещества после учета адсорбции растворителя
Рис. 1.51. Изотерма адсорбции растворенного вещества после учета адсорбции растворителя
