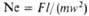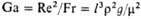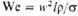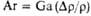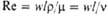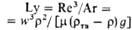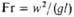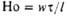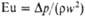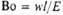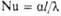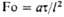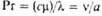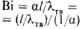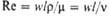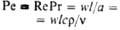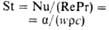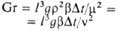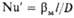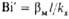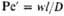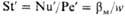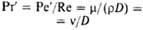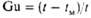Подобия теория
ПОДОБИЯ ТЕОРИЯ, учение об условиях подобия разл. объектов (физ. явлений, процессов, аппаратов, систем), отличающихся масштабами, геометрией или физ. природой. Осн. задачи подобия теории: установление критериев подобия разных объектов, изучение их CB-B с помощью этих критериев, определение возможности обобщения результатов решения конкретных задач при отсутствии способов нахождения их полных решений. Успехи в развитии подобия теории связаны с именами И. Ньютона, Ж. Фурье, Дж. Рэлея, T. Афанасьевой-Эренфест, M. Рябушинского, P. Бэкингема, П. Бриджмена, M. В. Кирпичева, А. А. Гухмана, Г. К. Дьяконова, Л. И. Седова и др.
Два объекта подобны, если в соответствующие (сходственные) моменты времени в соответствующих точках пространства значения переменных величин, характеризующих состояние одного объекта, пропорциональны значениям соответствующих величин др. объекта. Коэф. пропорциональности соответствующих величин наз. коэффициентами подобия.
Виды подобия. Различают геом., физ., физ.-хим. и мат. подобие. При геом. подобии пропорциональны геом. характеристики соответствующих элементов объектов (напр., длины, высоты или диаметры аппаратов). При физ. подобии в пространстве и времени подобны поля соответствующих физ. параметров двух объектов, напр. при кинематич. подобии-поля скоростей, при динамич. подобии-системы действующих сил или силовых полей (силы инерции, тяжести, вязкости, давления и др.); при мех. или гидромех. подобии, предполагающем наличие геом., кинематич. и динамич. подобия,-упругие системы, потоки жидкостей, газов или их смесей и др.; при подобии тепловых процессов-соответствующие поля т-р и тепловых потоков; при подобии массооб-менных процессов-потоки в-в и поля их концентраций и др.; при подобии хим. процессов - поля концентраций, т-р и др.; при электродинамич. подобии-поля токов, нагрузок, мощностей, электромагн. сил. Для сложных физ. и физ.-хим. процессов, включающих мех., гидромех., тепло- и массо-обменные, а также хим. явления, подобия теория устанавливает условия подобия, напр. процессов трения при движении материальных потоков в трубах, каналах и аппаратах, кинетики физ.-хим. превращений и др. явлений. При мат. подобии рассматриваемые объекты описываются одинаковыми ур-ниями, что позволяет говорить, напр., о подобии тепловых и массообменных процессов, и т.п.
Анализ размерностей и нормализация уравнений взаимосвязи физических величин. Осн. метод подобия теории-анализ размерностей физ. величин, характеризующих состояние объекта исследования, и параметров, к-рые определяют это состояние. Под размерностью физ. величины понимают выражение связи между ней и физ. величинами, положенными в основу системы единиц. Анализ размерностей позволяет определять вид таких ур-ний взаимосвязи физ. величин в изучаемых явлениях. Базой анализа размерностей служит требование, согласно к-рому осн. ур-ния, выражающие связь между переменными и параметрами объекта, должны быть справедливы при любом выборе единиц измерения входящих в них величин; значения переменных определяются решением данной системы ур-ний, значения параметров должны быть заданы для решения этой системы. Из этого требования следует, в общем, что все слагаемые - каждого ур-ния должны иметь одинаковые размерности и, в частности, что с помощью операции, наз. нормализацией (преобразованием), м. б. приведены к безразмерному виду.
Нормализацию обычно проводят в два этапа. На первом этапе все переменные преобразуются к безразмерному виду путем выбора соответствующих масштабов так, чтобы диапазоны изменения всех безразмерных переменных были одинаковы (напр., равны 1). При этом масштабные коэф. переменных включают в состав коэф. соответствующих членов нормализуемого ур-ния. На втором этапе все члены ур-ния делят на один из коэф., что дает возможность сделать каждый член ур-ния безразмерным. Если ур-ние имеет начальные и граничные условия, то и они соотв. преобразуются.
Свойства нормализованных уравнений. Эти ур-ния содержат, как правило, величины двух типов: а) безразмерные зависимые и независимые переменные; б) безразмерные параметры (иногда наз. p-комплексами). Последние включают характерные размеры (масштабы) объекта, а также физ. параметры исходного ур-ния и граничных условий. Объекты, описание Cв-в к-рых сводится к одинаковым безразмерным ур-ниям и граничным условиям, независимо от их физ. природы относятся к одному классу. Очевидно, что геометрически подобные или даже физически идентичные системы нельзя относить к одному классу, если граничные условия для них не будут представлены одинаково (напр., при разл. профилях скоростей потока на входе в идентичные аппараты).
Объекты, относящиеся к одному классу и имеющие одинаковые численные значения p-комплексов в ур-ниях и соответствующих граничных условиях, подобны, поскольку поля изменения физ. характеристик, определяемые безразмерными переменными, отличаются лишь выбранными масштабными коэф., отношения к-рых задают коэф. подобия. Поэтому p-комплексы наз. также критериями или числами подобия, равенство к-рых для объектов, описываемых идентичными безразмерными ур-ниями и граничными условиями, обеспечивает их подобие.
Изменение значений критериев подобия означает переход от одного объекта к другому в пределах объектов данного класса. При таком переходе условия подобия не соблюдаются, только при относительно небольших изменениях критериев или изменениях тех из них, к-рые слабо влияют на решение ур-ний, можно говорить о неполном, или частичном, подобии. Такие случаи чаще всего встречаются на практике при изучении подобия реальных объектов. Напр., при изменении геом. размеров технол. установки затрудняется соблюдение постоянства критериев подобия, включающих объемные и поверхностные характеристики аппаратов, т. к. отношение объема к поверхности изменяется пропорционально их размерам.
Размерные физ. параметры, входящие в критерии подобия, для подобных объектов могут иметь сильно различающиеся значения; важно только, чтобы мало отличались друг от друга значения самих критериев. Именно это св-во подобных систем составляет основу метода моделирования и позволяет корректно решать задачи масштабирования, т. е. использовать результаты исследований одного объекта при изучении другого, полностью или частично ему подобного, хотя и существенно отличающегося размерами либо режимами работы. Поэтому соблюдение постоянства критериев подобия - решающее условие успешного переноса исследований на иные объекты (см. также Масштабный переход).
Анализ решения нормализованных уравнений. Важное следствие процедуры нормализации состоит в том, что число критериев подобия в безразмерных ур-ниях и их граничных условиях всегда оказывается меньше числа физ. параметров, входящих в исходные соотношения. С одной стороны, это устанавливает необходимое кол-во критериев подобия разл. объектов, принадлежащих к одному классу, с другой - упрощает до нек-рой степени решение целого ряда сложных задач.
Решения безразмерных ур-ний с соответствующими граничными условиями определяют безразмерные переменные объекта как ф-ции независимых переменных и критериев:
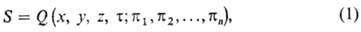
где х, у, z - безразмерные пространств. координаты; т-безразмерная переменная, соответствующая времени; p1-pn-критерии подобия.
Безразмерный вид ф-ции 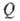 зависит от вида ур-ний и граничных условий и обычно не м. б. записан в общей форме. Однако сам факт существования зависимости (1) приводит к разл. выводам. Напр., при решении задачи оценки нек-рых параметров начальных ур-ний по опытным данным выражение (1) позволяет установить, какими критериями определяется безразмерный комплекс, включающий неизвестный параметр. Далее можно попытаться найти данную связь в виде нек-рой принятой (напр., степенной) функцион. зависимости от остальных критериев. Для этого выполняют необходимый объем экспериментов в разл. условиях (при к-рых изменяются значения критериев) и с помощью выбранной зависимости осуществляют соответствующие расчеты наблюдаемых результатов. Полученное соотношение м. б. использовано уже для анализа целой группы объектов, критерии подобия к-рой отвечают изученной области изменения их значений. Такие исследования часто проводят при решении проблем гидромеханики, тепло- и массообмена и т. п. в химико-технол. процессах.
зависит от вида ур-ний и граничных условий и обычно не м. б. записан в общей форме. Однако сам факт существования зависимости (1) приводит к разл. выводам. Напр., при решении задачи оценки нек-рых параметров начальных ур-ний по опытным данным выражение (1) позволяет установить, какими критериями определяется безразмерный комплекс, включающий неизвестный параметр. Далее можно попытаться найти данную связь в виде нек-рой принятой (напр., степенной) функцион. зависимости от остальных критериев. Для этого выполняют необходимый объем экспериментов в разл. условиях (при к-рых изменяются значения критериев) и с помощью выбранной зависимости осуществляют соответствующие расчеты наблюдаемых результатов. Полученное соотношение м. б. использовано уже для анализа целой группы объектов, критерии подобия к-рой отвечают изученной области изменения их значений. Такие исследования часто проводят при решении проблем гидромеханики, тепло- и массообмена и т. п. в химико-технол. процессах.
Метод подобия. На практике не всегда удается записать в явном виде полную систему ур-ний, достаточно точно отражающую св-ва объекта, и определить из нее критерии подобия. Одним из методов, позволяющих в этих условиях получить информацию о количеств.оценке подобия, является основанный на использовании соотношений сил, действующих в объекте, т. наз. метод подобия. Последний предполагает, что два объекта подобны, если выполняется их геом., кинематич. и динамич. подобие, причем для соблюдения этих условий достаточно геом. подобия и равенства соотношений всех сил, существующих для данных объектов.
Метод включает след. операции. 1) В рассматриваемом объекте перечисляют силы, к-рые считают наиб. существенными, в т. ч. все независимые и зависимые силы. Каждую из выбранных сил выражают через физ. параметры объекта на основе физ. представлений и соображений размерности. 2) Безразмерные критерии, характеризующие задачу, определяют как соотношения сил. Число критериев, к-рые можно из них образовать, равно числу независимых сил. 3) Для учета геом. подобия составляют соотношения линейных размеров.
Описанный метод представляет чисто механистич. подход к анализу объектов и не согласуется с принципами термодинамики. Поэтому, получив довольно широкое применение в гидродинамике, он оказался практически бесполезен, напр., для решения задач тепло- и массообмена в химико-технол. процессах, поскольку переносимые в них потоки теплоты и массы вообще не зависят от сил, действующих в соответствующих объектах.
Для распространения этого метода на тепловые и по аналогии также на массообменные (диффузионные) процессы предложен обобщенный метод подобия, в к-ром в рассмотрение введены соотношения разл. общих форм энергии (мех., тепловой, хим. и др.). Метод предполагает, что для подобия двух объектов кроме геом. подобия и равенства соотношений сил необходимо также обеспечить подобие соотношений соответствующих энергий.
Применение указанных соотношений линейных размеров, сил или энергий позволяет образовать соответствующие безразмерные отношения - критерии подобия для разл. процессов. Так, в гидродинамике принято рассматривать шесть общих сил, действующих в потоке жидкости или газа: инерции (Fи), трения, или вязкости (FT), давления (Fд), упругости (Fy), поверхностного натяжения (Fп.н. ), гравитации (Fг). C использованием этих сил можно образовать 15 соотношений из двух сил: Fи/Fп.н., FM/Fy, FM/FT, Fд/FT, FM/Fг, Fд1/Fи и т.д. Поскольку отдельные критерии определяются как соотношения независимых сил, одни критерии м. б. выражены через другие; при этом любая комбинация из критериев подобия также представляет собой критерий подобия рассматриваемых физ. явлений. Сходным путем составляют критерии теплового подобия и их диффузионные аналоги.
Для критериев (чисел) подобия принята спец. система обозначений в виде двух первых букв, как правило, фамилий ученых, внесших значит. вклад в данную область знания, и соответствующих наименований. Каждый из критериев подобия имеет определенный физ. смысл как величина, пропорциональная соотношению однотипных физ. величин. Сводка наиб. распространенных в хим. технологии критериев (чисел) подобия и входящих в них величин представлена в таблицах (см. также, напр., Гидромеханические процессы, Макрокинетика, Массообмен, Теплообмен).
ОСНОВНЫЕ КРИТЕРИИ ПОДОБИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
| Число | Ф-ла | Физ. смысл | Число | Ф-ла | Физ. смысл |
| | | Гидромеханич. процессы | | ||
| Ньютона | | Мера соотношения действующей на систему силы и силы инерции | Галилея | | Характеризует влияние сил тяжести и инерции при естеств. конвекции |
| Вебера | | Мера соотношения сил инерции и поверхностного натяжения; отражает влияние последней на движение потока | Архимеда | | Характеризует влияние на силу тяжести плотности потока при естеств. конвекции |
| Рейнольдса | | Мера соотношения сил инерции и вязкости; отражает влияние силы трения на движение потока | Лященко | | Характеризует влияние силы тяжести на осаждение твердых частиц в потоке |
| Фруда | | Мера соотношения сил инерции и тяжести; отражает влияние последней на движение потока | Гомохрон-ности | | Характеризует одинаковость протекания процессов во времени при нестационарном движении потока |
| Эйлера | | Мера соотношения между изменением силы гидростатич. давления и силой инерции; отражает влияние перепада давления на движение потока | Боден-штейна | | Характеризует влияние продольного перемешивания на градиенты концентраций в-в в потоке |
| Маха | M = w/w3 | Характеризует влияние сжимаемости потока на его движение | |||
| | | Тепловые процессы | | | |
| Нуссельта | | Мера интенсивности теплоотдачи на границе раздела фаз | Фурье | | Характеризует нестационарность переноса теплоты путем теплопроводности при изменении т-ры во времени |
| Прандтля | | Мера соотношения вязкостных и темпера-туропроводных св-в теплоносителей; мера соотношения полей скоростей и т-р в потоке | Био | | Характеризует постоянство соотношения внутр. термич. сопротивления нестационарной теплопроводности к внеш. термич. сопротивлению теплоотдаче |
| Рейнольдса | | Характеризует режим движения теплоносителей (см. также выше) | | | |
| Пекле | | Мера соотношения теплот, переносимых конвекцией и теплопроводностью | Стантона (Стэнтона) | | Характеризует соотношение кол-в теплот, переносимых конвекцией и движущимся потоком жидкости (газа); интенсивность диссипации энергии в потоке |
| Грасгофа | | Мера соотношения сил трения, инерции и подъемной (архимедовой) силы, определяемой разностью плотностей в разл. точках неизотермич. потока при своб. конвекции | | | |
| | | Массообменные (диффузионные) процессы | | ||
| Нуссельта * | | Безразмерный коэф. массоотдачи | Био | | Мера соотношения внутри- и внешнедиф-фузионных сопротивлений при массопере-даче с участием твердой фазы |
| Пекле | | Мера соотношения масе в-ва, переносимых конвекцией и путем мол. диффузии | Стантона (Стэнтона) | | Характеризует подобие полей концентраций и скоростей в турбулентных потоках |
| Прандтля * | | Мера постоянства соотношений физ. св-в жидкостей (газов) в подобных потоках; мера подобия профилей скоростей и концентраций в процессах массоотдачи | Гухмана | | Мера соотношения потенциала сушки и т-ры среды; отражает влияние массообмена на теплообмен |
| Фурье | | Характеризует изменение во времени скорости переноса в-ва при нестационарной массоотдаче | | | |
* В зарубежной литературе Nu'-число Шервуда (Sh); Pr-число Шмидта (Sc).
Общий недостаток рассмотренных методов подобия-неопределенность конкретных масштабов физ. величин, что особенно важно при решении реальных задач. Поэтому указанными критериями подобия, как правило, нельзя пользоваться без спец. проверки. Кроме того, выбор масштабов во мн. случаях довольно затруднителен.
ВЕЛИЧИНЫ, ВХОДЯЩИЕ В КРИТЕРИИ ПОДОБИЯ
| Величина | Обозначение | Единица измерения | | Величина | Обоозна- чение | Едини-ца из-мерения | ||
| Время | т | с | | Масса | m | кг | ||
| Давление, разность давлений | p, Dp | Па | | Определяющий геом. размер | l | м | ||
| Динамич. вязкость | m | Па·с | | Плоти, жидкости (газа) и твердого тела | r, rтв | кг/м3 | ||
| Кинематич. вязкость | v | м2/с | ||||||
| | Поверхностное натяжение | s | Н/м | |||||
| Коэф. диффузии | D | м2/с | ||||||
| Коэф. массоотдачи | bм | В зависимости от способа выражения состава фаз | | Сила | F | H | ||
| | Скорость, скорость звука | w,w3 | м/с | |||||
| | Т-ра, разность т-р, т-ра мокрого термометра | t, Dt, tм | К | |||||
| Коэф. массопро-водности | ks | м2/с | ||||||
| | Уд. теплоемкость (при постоянном давлении) | с | Дж/(кг·К) | |||||
| Коэф. объемного расширения | bоб | К-1 | | |||||
| Коэф. температуропроводности | a | м2/с | | Ускорение своб. падения | g | м/с2 | ||
| Коэф. теплоотдачи | a | Вт/ (м2 ·К) | | Фиктивный коэф. диффузии (коэф. продольного перемешивания) | E | м2/с | ||
| Коэф. теплопроводности жидкости (газа) и твердого тела | l, lтв | Вт/ (м ·К) | | |||||
p-Теорема. Иной подход к установлению подобия разных объектов основан на применении т. наз. p-теоремы, к-рая связывает ф-ции, выраженные соотв. через размерные физ. параметры и безразмерные p-комплексы. Формулировка p-тсормы: если имеется соотношение между m размерными параметрами в виде:
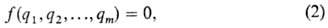
то можно найти эквивалентные соотношения между n безразмерными параметрами в виде:
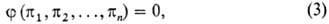
где n = т — k, причем k-наиб. число параметров, входящих в ур-ние (2), к-рые нельзя объединить в к.-л. безразмерный комплекс. Число k обычно равно числу независимых размерностей r, необходимых для образования всех размерностей параметров q; в нек-рых исключит. случаях
Использование p-теоремы позволяет за счет применения безразмерных комплексов уменьшить число независимых параметров при решении реальных задач, а также обеспечить возможность сопоставлять и обобщать результаты решений. Однако и данный метод отличают недостатки: 1) отсутствуют прямые способы нахождения определяющих параметров, и метод фактически используют после того, как эти параметры найдены; 2) теорема не указывает условий, при к-рых можно пренебречь нек-рыми p-комплексами, что существенно при задании правил приближенного подобия; 3) из теоремы не ясны способы определения наиб. важных для данной задачи безразмерных комплексов и нельзя установить, какие из них обеспечат лучшие соотношения для частных задач.
Применение теории. Среди методов, используемых в подобия теории, от перечисл. недостатков до нек-рой степени свободен описанный выше метод, основанный на нормализации и анализе общих ур-ний. Но и этот метод требует для записи общих ур-ний полной информации об определяющих параметрах, включая сведения о механизмах процессов, к-рые протекают в исследуемых объектах. Вместе с тем области практич. применения подобия теории достаточно широки. Она позволяет проводить предварит. качественно-теоретич. анализ и зачастую является основой для постановки опытов и обработки полученных данных. Кроме того, подобия теория оказывается полезной при выполнении численных экспериментов в мат. моделировании и интерпретации его результатов.
Лит.: Клайн С.-Дж., Подобие и приближенные методы, пер. с англ., M., 1968; Касаткин А. Г., Основные процессы и аппараты химической технологии, 9 изд., M., 1973, с. 64-84, 279-83, 401-06; Коган В. Б., Теоретические основы типовых процессов химической технологии, Л., 1977, с. 69-83; Гельперин H. И., Основные процессы и аппараты химической технологии, M., 1981, кн. 1, с. 42-45, 278-85, кн. 2, с. 446-48; Седов Л. И., Методы подобия и размерности в механике, 9 изд., M., 1981. А. И. Бояринов.