4.2.2. Элементарная теория электрокинетических явлений
Причина возникновения электрокинетических явлений лежит в существовании двойного слоя и нарушении его электронейтральности в электрическом поле. Если поместить в U-образную трубку мелкий кварцевый песок, краситель, пигмент или волокно, налить раствор и, погрузив электроды, пропускать электрический ток, то уровень воды у одного из электродов, преимущественно отрицательного полюса, повышается. Это явление одностороннего перемещения воды под влиянием электрического тока, названное электроосмосом, можно объяснить, если рассмотреть процессы, происходящие в одном из мельчайших капилляров, пронизывающих образующуюся мембрану. На границе твердой фазы с водой за счет диссоциации поверхностных ионогенных групп возникает двойной слой, внутренняя обкладка которого образована отрицательно заряженными группами -SiO22-у кварца, -СОО- - у волокна. Наружный слой, как правило, состоит из ионов Na+. Непрочно связанные с поверхностью ионы диффузной части двойного слоя под влиянием внешнего электрического поля оторвутся и будут перемещаться к отрицательному электроду. Направленное движение этих ионов вызовет за счет трения движение жидкости, заполняющей капилляр. В результате такого явления, проявляющегося во всех многочисленных капиллярах диафрагмы, наблюдается одностороннее перемещение жидкости к одному из электродов.
Перемещение частиц дисперсной фазы в электрическом поле к одному из электродов, называемое электрофорезом, также является следствием нарушения электронейтральности двойного слоя. Без действия внешнего электрического поля двойной слой электронейтрален. При наложении разности потенциалов происходит разрыв двойного слоя по плоскости скольжения и частицы перемещаются тем быстрее, чем выше градиент потенциала. Частица, лишенная диффузной ионной оболочки, приобретает отрицательный заряд и будет перемещаться к положительному электроду. Измеренный по скорости перемещения частиц электрокинетический потенциал следует исправлять, учитывая сопротивление электроосмотического перемещения дисперсионной среды.
При определении электрокинетического потенциала методом электоосмоса делаются следующие предпосылки в соответствии с теорией Гельмгольца строения двойного ионного слоя.
1. Двойной ионный слой представляют в виде плоского параллельного конденсатора, внутренняя обкладка которого представлена зарядами поверхности твердого тела, внешняя - зарядами, локализованными в жидкости. Толщина этого слоя (конденсатора) такова, что включает в себя лишь несколько молекулярных слоев и меньше радиуса капилляра.
2. Слой жидкости, непосредственно прилегающий к твердой поверхности, при электрокинетических явлениях остается неподвижным, тогда как все последующие слои перемещаются. Течение жидкости происходит в ламинарном режиме и описывается обычными уравнениями гидродинамики.
3. Стенка капилляра не проводит электрический ток и слой потенциалопределяющих ионов локализован, т.е. не может перемещаться по поверхности.
4. Внешняя разность потенциалов суммируется как аддитивная величина с перепадом потенциала в двойном слое. Это означает, что внешнее поле не деформирует двойного слоя, не нарушает его равновесия, хотя и обеспечивает непрерывное перемещение заряженного слоя жидкости вдоль поверхности.
Поскольку эта предпосылка предполагает постоянное восстановление равновесия в двойном слое в процессе электроосмоса, такая система может рассматриваться как конденсатор, пластины которого, находящиеся на расстоянии d, заряжены с поверхностной плотностью r. Данным значениям d и r соответствует разность потенциала между пластинами z. Поскольку толщина двойного слоя мала, то кривизной капилляра пренебрегают (считая, что слой плоский) и разрыв его в электрическом поле с градиентом потенциала Н= Е/l происходит по плоскости на расстоянии d от поверхности.
В таком случае напряжение сдвига в расчете на единицу площади поверхности, заставляющее жидкость двигаться,
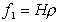 . (1.4.11)
. (1.4.11)
Это напряжение будет уравновешиваться сопротивлением ламинарного потока, т.е. силой трения
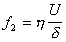 , (1.4.12)
, (1.4.12)
где h -вязкость жидкости, U- скорость перемещения жидкости в капилляре, U/d - градиент скорости в направлении, перпендикулярном к твердой поверхности.
При стационарном режиме течения 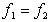 , т.е.
, т.е.
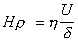 . (1.4.13)
. (1.4.13)
Учитывая, что для плоского конденсатора
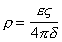 , (1.4.14)
, (1.4.14)
получаем для скорости течения
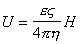 . (1.4.15)
. (1.4.15)
Количество жидкости, переносимое через капилляр, т.е. объемная скорость течения,
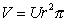 . (1.4.16)
. (1.4.16)
Поэтому
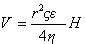 . (1.4.17)
. (1.4.17)
Естественно, что на практике не используют для измерений один капилляр, а изготавливают из непроводящего электрический ток материала мембрану толщиной l со множеством капилляров общим сечением 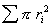 . Это сечение определяют по электрическому сопротивлению диафрагмы R, капилляры которой заполнены раствором с электропроводимостью k :
. Это сечение определяют по электрическому сопротивлению диафрагмы R, капилляры которой заполнены раствором с электропроводимостью k :
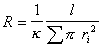 . (1.1.18)
. (1.1.18)
В соответствии c законом Ома 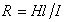 , где
, где 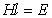 - разность потенциалов, приложенных к обеим сторонам мембраны, а I– сила тока.
- разность потенциалов, приложенных к обеим сторонам мембраны, а I– сила тока.
Следовательно,
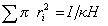 . (1.4.19)
. (1.4.19)
Заменяя в (1.4.16) 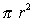 на
на 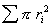 и используя (1.4.19), получаем
и используя (1.4.19), получаем
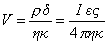 (1.4.20)
(1.4.20)
При использовании для расчетов формулы (1.4.20) следует учитывать, что величины h, kи e двойного слоя могут отличаться от величин, характерных для большого объема жидкости. С этой целью иногда вводится поправка на поверхностную проводимость ks, использовать которую предложил еще Смолуховский для учета конвективного потока ионов вдоль стенки капилляра, что возможно, выразив общую проводимость k узкого капилляра формулой
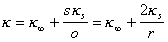 , (1.4.21)
, (1.4.21)
где s- периметр; o- сечение капилляра; 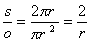 .
.
Из уравнения (1.4.21) видно, что разность 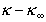 уменьшается с увеличением радиуса капилляра и
уменьшается с увеличением радиуса капилляра и 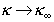 , т.е. при определенных условиях электропроводность в пределах двойного слоя стремится к величине ее в объеме раствора.
, т.е. при определенных условиях электропроводность в пределах двойного слоя стремится к величине ее в объеме раствора.
Формула (1.4.20) применима при любом расположении капилляров в мембране, так как и электрический ток, и электроосмотический поток движутся параллельно стенкам капилляра.
Электроосмос не связан со структурой межфазной поверхности, но зависит от таких характеристик двойного слоя, как ks, e, d, r. Приведенные выше уравнения могут быть использованы и для расчета электрокинетического потенциала по скорости электрофореза. Механизм этого явления подобен механизму электроосмоса, но в данном случае неподвижной остается дисперсионная среда, а перемещаются частицы. Электрофоретическую скорость перемещения (подвижность) частиц Uef можно рассчитать, как U/H. Эта величина характеризует подвижность коллоидной частицы при электрофорезе. В принципе, она аналогична подвижности ионов в электрическом поле, поэтому
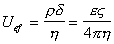 . (1.4.22)
. (1.4.22)
Эта формула не учитывает влияния ионной атмосферы на электрофоретическую подвижность и формы частиц. Более правильно следует записать ее, как предложил Генри (1931 г.),
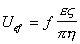 (1.4.23)
(1.4.23)
где f- сила электрофоретического торможения, которая зависит от радиуса частиц и радиуса ионной атмосферы (фактора Дебая) k. Для цилиндрических частиц, ось которых ориентирована по направлению электрического поля, f = 1/4. Если ось перпендикулярна к полю, f = 1/8. Для сферических частиц f = 1/6 и стремится к 1/4 при больших значениях kr. Все это справедливо для частиц, не проводящих электрический ток. Кроме того, при утолщении двойного ионного слоя становится некорректным рассмотрение гидродинамических и электрических явлений порознь внутри и вне двойного слоя, как это делал Смолуховский. Потенциал течения способен возникать в том случае, если при воздействии силового механического поля течение жидкости увлекает ионы диффузионной обкладки двойного слоя, так что вдоль стенки капилляра возникает стационарный поток ионов. Если вдоль капилляра существует градиент давления dP/dl, где l – длина капилляра, то возникает течение, которое в соответствии с законом Пуазейля при x где x- расстояние потока от стенки капилляра. Для цилиндрического капилляра с постоянным сечением dP/dl = DP/l, где DP- разность давлений на концах капилляра, на расстоянии d< Возникающий при этом конвективный ток Ic определяется количеством свободных зарядов на 1м2 слоя, движущихся на расстоянии d со скоростью Ud.: Перенос электрического заряда вызывает разность потенциалов E=Hl на концах капилляра, которая, в свою очередь, вызывает протекание нарастающего тока проводимости через раствор с сопротивлением R. Когда ток проводимости становится равным конвективному потоку, разность потенциалов приобретает постоянное стационарное значение, равное потенциалу течения DVst. Согласно закону Ома Приравнивая (1.4.26) и (1.4.27) и подставляя (1.4.25), получаем В этом выражении для поверхностной плотности заряда использовалось выражение (1.4.14). Формула (1.4.28) справедлива и для случая пористой перегородки с капиллярами произвольной формы. Если сопоставить результаты измерения потенциала течения и электроосмотической скорости для одной и той же системы, то получим Седиментационный поток частиц относительно неподвижной жидкости возбуждает конвективный поток ионов диффузионного двойного слоя. Поле, которое при этом возникает, препятствует этому перемещению. Поэтому, по аналогии с приведенным выше потенциалом течения, получим уравнение для расчета потенциала седиментации Esed. Скорость седиментации сферических частиц в соответствии с законом Стокса где r - радиус частиц; r2, r1- плотность дисперсной фазы и дисперсионной среды; g- ускорение силы тяжести. Если обозначить через q заряд одной частицы при седиментации и n- число частиц в единице объема, например 1 м3, то плотность конвективного потока (сила тока, проходящего через сечение площадью 1 м2) будет равна При стационарном режиме эта плотность равна плотности встречного тока проводимости Из условия стационарности Ic=Is , заменяя их на соответствующие величины из (1.4.31) и (1.4.32) и полагая, что Уравнение (1.4.33) справедливо для седиментации твердых частиц. При обратной седиментации при расчете потенциала для эффекта Дорна всплывающих газовых пузырьков или капелек жидкости необходимо учитывать сопутствующий электрокинетическим явлениям эффект диффузии ионов. При движении твердых частиц в растворе электролита возникает разность концентраций между полюсами по направлению движения частиц и проявляется диффузионный потенциал. Только при равенстве коэффициентов диффузии катионов и анионов в классические уравнения не вводятся поправки. Во всех остальных случаях уравнения должны быть откорректированы. 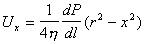 , (1.4.24)
, (1.4.24)
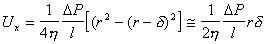 . (1.4.25)
. (1.4.25)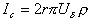 . (1.4.26)
. (1.4.26)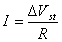 при
при 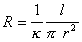 . (1.4.27)
. (1.4.27)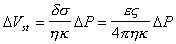 . (1.4.28)
. (1.4.28)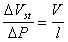 . (1.4.29)
. (1.4.29)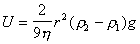 , (1.4.30)
, (1.4.30) 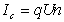 . (1.4.31)
. (1.4.31)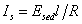 ; здесь
; здесь 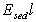 - стационарная разность потенциалов между электродами, находящимися на расстоянии l друг от друга. Связь заряда сферической частицы q и z-потенциала можно записать, исходя из равенства между электрической силой qE, действующей при электрофорезе, и силой трения
- стационарная разность потенциалов между электродами, находящимися на расстоянии l друг от друга. Связь заряда сферической частицы q и z-потенциала можно записать, исходя из равенства между электрической силой qE, действующей при электрофорезе, и силой трения 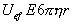 , возникающей при движении частиц со скоростью
, возникающей при движении частиц со скоростью 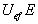 . Таким образом получаем
. Таким образом получаем 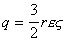 . (1.4.32)
. (1.4.32)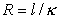 , получаем
, получаем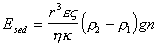 . (1.4.33)
. (1.4.33)


