Многокомпонентные системы

МНОГОКОМПОНЕНТНЫЕ СИСТЕМЫ, физ.-хим. системы, содержащие не менее трех компонентов. Компонентами системы наз. в-ва, изменения масс к-рых независимы и выражают все возможные изменения в составе системы. Если в системе отсутствуют обратимые хим. р-ции, число компонентов равно числу в-в, содержащихся в системе. В случае систем с хим. превращениями число компонентов равно разности между числом сортов частиц, содержащихся в системе, и числом независимых р-ций. Это объясняется тем, что условия хим. равновесия выражаются как количеств. связи между концентрациями в-в, а число таких связей равно числу независимых хим. р-ций.

Число компонентов, вообще говоря, зависит от условий, в к-рых находится система. Изменяя условия, можно инициировать или тормозить хим. р-ции и тем самым менять число связей, накладываемых на изменения концентраций в-в. Число компонентов может зависеть от точности экспе-рим. исследования, т.к. в отдельных случаях требуется

учитывать концентрации в-в, присутствующих в очень малых кол-вах. Числа молей всех компонентов m_i (i = 1, 2,..., n)характеризуют не только соотношение между ними, но и общую массу n-компонентной системы (фазы). Поэтому для задания состава многокомпонентных систем чаще используют молярные доли компонентов x_i = m_i /(m₁ + т₂ + ... + m_n), к-рые подчинены условию x₁ + х₂ + ... + x_n = 1, и, следовательно, только (п — 1) из них являются независимыми.

В случае тройных систем состав смеси изображают с помощью концентрац. треугольника Гиббса-Розебома. Вершины треугольника отвечают чистым компонентам, точки на сторонах - составам двойных (бинарных) систем; точки внутри треугольника характеризуют состав тройной смеси, причем молярная доля данного компонента пропорциональна длине перпендикуляра, опущенного из точки состава на сторону треугольника, противолежащую вершине этого компонента.

Состав четверной системы м.б. изображен с помощью правильного тетраэдра. Вершины тетраэдра соответствуют чистым компонентам, точки на ребрах-составам двойных систем, точки на гранях-составам тройных систем, пространство внутри тетраэдра - четверным смесям. Молярная доля данного компонента в четверной смеси пропорциональна расстоянию от точки состава до грани, противолежащей вершине этого компонента.

Важное практич. значение имеет исследование четверных водно-солевых систем, представляющих собой водные р-ры солей АХ, ВХ, СХ или АХ, AY, AZ. Такие смеси обычно обозначают А, В, С||Х-Н₂О и А||Х, Y, Z-H₂O, отделяя катионы от анионов двойной вертикальной чертой. Для таких систем вместо молярных долей компонентов обычно используют т.наз. координаты Йенеке. Их определяют, принимая сумму концентраций солей в молях за 100% (т.наз. солевая масса) и нанося солевой состав на треугольник Гиббса-Розебома. Вдоль линий, перпендикулярных плоскости треугольника, откладывают число молей воды, приходящихся на 100 молей солевой массы; это т.наз. в о д н о с т ь системы. Концентрации солей в солевой массе наз. и н д е к с а м и Й е н е к е солей; вместе с водностью они и составляют координаты Йенеке.

В з а и м н ы м и в о д н о-с о л е в ы м и с и с т е м а м и наз. четверные системы A,B||X,Y-H₂O, в к-рых имеет место р-ция обмена АХ+ BY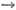AY + ВХ. Их характеризуют обычно индексами Йенеке одного из катионов и одного из анионов (сумма эквивалентов всех ионов принимается равной 100) и водностью. Концентрац. пространством, характеризующим солевой состав взаимных систем, является квадрат (как в тройных взаимных системах А, В||Х, Y).

При дальнейшем увеличении числа компонентов в системе размерность концентрац. пространства соотв. возрастает, что неизбежно приводит к использованию разрезов и разл. проекций на подпространства меньшей размерности. Необходимость в проекциях и сечениях еще больше возрастает при графич. изображении разл. физ.-хим. св-в системы, к-рые являются ф-циями ее состава (см. Диаграмма состав-свойство).

Наиб. важная физ.-хим. характеристика многокомпонентной системы-ее диаграмма состояния (фазовая диаграмма), определяющая фазовое состояние системы при разл. брутто-составе. В случае тройной системы с эвтектикой на фазовой диаграмме имеются пов-сти кристаллизации отдельных твердых фаз, линии, отвечающие совместной кристаллизации двух твердых фаз, и нонвариантная точка, отвечающая равновесию расплава с тремя твердыми фазами. Диаграмма плавкости тройной системы описывает т-ру плавления смесей разл. состава; она должна изображаться в трехмерном пространстве. На практике, однако, используют проекции изотермич. сечений этой диаграммы на плоскость концентрац. треугольника, а также сечения, отвечающие определенным соотношениям между концентрациями компонентов. В случае четверных и более многокомпонентных систем приходится строить проекции изотермич. сечений не на все концентрац. пространство, а на нек-рые из его подпространств меньшей размерности.

Диаграммы фазовых равновесий многокомпонентных систем являются теоретич. основой разделения в-в путем ректификации, экстракции, абсорбции, кристаллизации. Однако с увеличением числа компонентов эксперим. исследование фазовых равновесий значительно усложняется. В связи с этим важное значение приобретает разработка расчетных методов определения св-в многокомпонентных систем, в частности их фазовых диаграмм, по данным о св-вах подсистем с меньшим числом компонентов (см. Физико-химический анализ).

===
Исп. литература для статьи «МНОГОКОМПОНЕНТНЫЕ СИСТЕМЫ»: Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1-2, Л., 1967; Аносов В. Я., Озерова М. И., Фиалков Ю. Я., Основы физико-химического анализа, М., 1976; Новоселова А. В., Методы исследования гетерогенных равновесий, М., 1980; Рид Р., Праусниц Дж., Шервуд Т., Свойства газов и жидкостей, пер. с англ., Л., 1982. В. К. Филиппов.

Страница «МНОГОКОМПОНЕНТНЫЕ СИСТЕМЫ» подготовлена по материалам химической энциклопедии.