Межфазные скачки потенциала

МЕЖФАЗНЫЕ СКАЧКИ ПОТЕНЦИАЛА, разности элект-рич. потенциалов на границе раздела фаз электрод - электролит, обусловленные пространств. разделением зарядов и определяемые работой переноса через эту границу единичного воображаемого заряда. При переносе из бесконечно удаленной точки С, расположенной в вакууме, в точку А, находящуюся внутри нек-рой фазы а (напр., металла или р-ра электролита), Межфазные скачки потенциала наз. внутренним потенциалом фазы а и обозначается j^a (рис. 1). Он обусловлен своб. электростатич. зарядом самой фазы а, к-рый создает скачок потенциала Y^a, наз. внешним потенциалом фазы, и пространств. разделением связанных зарядов на границе вакуума и фазы а, в результате к-рого возникает п о в е р х н о с т н ы й п о т е н ц и а л Х^a. Следовательно, j^a = Y^a + Х^a.

Потенциал Y^a определяется работой переноса единичного воображаемого заряда из бесконечно удаленной точки С в вакууме в точку А', к-рая находится также в вакууме, но вблизи фазы а. Так, если фаза a-сфера радиуса R и несет своб. заряд Q, по законам электростатики Y^a = Q/4pe₀R, где e₀ = 8,854^.10^-12 Ф/м-электрич. постоянная (диэлектрич. проницаемость вакуума). Точка А' выбирается на таком малом расстоянии х от пов-сти фазы a, чтобы Q/4pe₀ (R + х)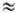 Q/4pe₀R, т. е. х << R. С др. стороны, х должно быть достаточно велико для того, чтобы можно было пренебречь взаимод. единичного заряда с индуцированным им зарядом внутри фазы а по сравнению с кулоновским взаимод. единичного заряда со своб. зарядом Q. Это условие выполняется при значениях х от 10^-7 до 10^-5 м (обычно полагают x 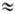10^-6м).

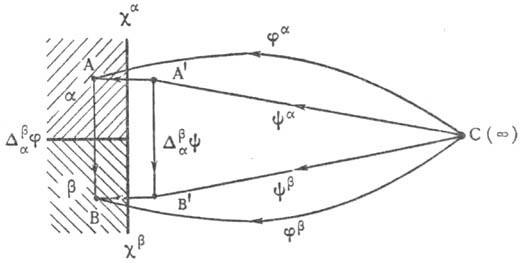
Рис. 1. Межфазные скачки потенциала при контакте фаз a и b.

Потенциал Х^a определяется работой переноса единичного воображаемого заряда из точки А' в точку А внутри фазы a. Если a-металл, Х^a возникает потому, что электронный газ выходит за пределы кристаллич. решетки металла и таким образом создается пространств. разделение зарядов; при этом Х^a > 0. Если же a- р-р электролита, механизм возникновения Х^a полагают следующим. Поскольку силы, действующие на первый слой молекул р-рителя со стороны вакуума (или воздуха) и со стороны р-ра, существенно различны, распределение частиц р-рителя вблизи пов-сти р-ра отличается от их хаотич. распределения в объеме р-ра. На пов-сти всегда возникает нек-рая предпочтит. ориентация молекул р-рителя и, если они полярны, т.е. обладают дипольным моментом, их ориентация может привести к пространств. разделению зарядов и возникновению разности потенциалов. С др. стороны, этот же эффект м. б. следствием неодинаковой сольватации анионов и катионов в р-ре и разл. расстоянием их центров заряда до границы раздела фаз в поверхностном слое р-ра.

Если фазы а и р контактируют, а точки В и В' находятся соотв. внутри фазы b и в вакууме на расстоянии х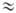 10 ^-6 м от ее пов-сти (рис. 1), то кроме описанных потенциалов фазы b (j^b, Y^b и Х^b) возникает также разность потенциалов между точками А и В, наз. гальвани-потенциалом (обозначается D_a^bj), и точками А' и В', наз. вольта-потенциалом (D_a^bY). Гальвани-потенциал определяется работой переноса единичного воображаемого заряда из точки А в точку В, вольта-потенциал-из А' в В'. Поскольку работа переноса заряда не зависит от пути переноса, галь-вани- и вольта-потенциалы можно записать как разность соответствующих внутренних или внешних потенциалов: D_a^bj = j^b - j^a; D_a^bY = Y^b - Y^a. Кроме того, как видно из рис. 1, D_a^bY = Х^a + D_a^bj - Х^b.

Поскольку в любом эксперименте по переносу зарядов через границу раздела фаз участвуют не единичные воображаемые заряды, а реальные заряженные частицы (электроны, ионы), всегда измеряется работа переноса этих частиц, определяемая разностью их электрохим. потенциалов в обеих фазах. По определению, электрохимический потенциал частицы i в фазе a m_i^a = m_i^a + z_iFj^a, где m_i^a-хим. потенциал этой частицы в фазе a, z,-ee зарядовое число, F- постоянная Фарадея. Работа переноса 1 моля частиц i из a в b равна: m_i^b — m_i^a = (m_i^b — m_i^a) + z_iF (j^b — j^a). Опытным путем разделить эту величину на две составляющие - химическую (m_i^b — m_i^a)и электрическую z_iF (j^b — j^a) - невозможно. Отсюда следует, что электрич. разность потенциалов между двумя точками м. б. измерена лишь при условии, что эти точки расположены в одинаковых по составу фазах, когда m_i^b — m_i^a = 0. Поэтому внутренние и поверхностные потенциалы, а также гальвани-потенциалы на границе двух фаз различного состава не м. б. измерены; внешние потенциалы и вольта-потенциалы доступны экспериментальному определению.

В обычных электрохим. экспериментах с помощью вольтметра или потенциометра всегда определяют разность потенциалов на концах правильно разомкнутой цепи, т. е. такой цепи, к-рая заканчивается проводниками из одного и того же металла. Обычно это достигается простым подключением к электродам Ml и М2 медных проводов (рис. 2, а). Такая цепь имеет четыре гальвани-потенциала: D^M1_Cuj, D^p-p_M1j, D^M2_p-pj и D^Cu_M2j. Можно, однако, показать, что эта цепь эквивалентна цепи, изображенной на рис. 2, в и содержащей только три гальвани-потенциала: D^M1_M2j, D^p-p_M1j и D^M2_p-pj. Действительно, включение между медным проводом и металлом Ml проводника из металла М2 (рис. 2,6)не изменяет разности потенциалов на концах цепи. Поэтому цепи на рис. 2, а и 2,б эквивалентны. Но цепь на рис. 2,б одновременно эквивалентна и цепи на рис. 2, в, т. к. отличается от нее двумя гальвани-потенциалами D^M2_Cuj, к-рые в точности компенсируют друг друга. Следовательно, эквивалентны и цепи, изображенные на рис. 2, а и 2, в.

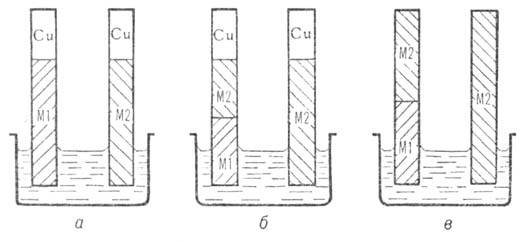
Рис. 2. Эквивалентные правильно разомкнутые электрохим. цепи.

Хотя абс. значения Х^a и D^b_aj нельзя измерить, можно определить на опыте их изменения. Так, если в системе (рис. 2,а)электрич. состояние металла Ml оставить без изменения, а М2 изменить поляризацией от внеш. источника путем погружения в р-р третьего вспомогат. электрода, то изменение разности потенциалов между двумя первыми электродами будет равно изменению гальвани-потенциала D^M2_p-pj.

Поверхностные потенциалы следует отличать от доступной измерению работы выхода W^a_i частицы i, т.е. работы переноса ее из фазы а в точку А', расположенную в вакууме на расстоянии х от границы раздела фаз. Для 1 моля частиц W^a_i = — m^a_i — z_iFX^a. Если объемный состав фазы а не изменяется и, следовательно, m^a_i = const, а поверхностный потенциал этой фазы изменяется, напр., вследствие адсорбции к.-л. в-ва, то изменение Х^a однозначно связано с изменением W^a_i ф-лой dХ^a = — dW^a_i/z_iF. Эта ф-ла лежит в основе эксперим. определения dХ^a.

Для оценки абс. значения X^a пользуются модельными расчетами. При этом задаются моделью границы фазы а с вакуумом и по распределению заряженных частиц на этой границе рассчитывают Х^a (или задаются моделью объема фазы а, рассчитывают на ее основе m^a_i) и с помощью найденного экспериментально значения W^a_i рассчитывают Х^a по ф-ле Х^a = - (m^a_i+ W^a_i)/z_iF. Если оба из указанных способов дают согласующиеся значения, оценку можно считать достаточно надежной.

Для модельного расчета гальвани-потенциала используют ф-лу: D^b_aj = D^b_aY + Х^b — Х^a, в к-рую подставляют найденный экспериментально вольта-потенциал и значения Х^b и Х^a, полученные на основе модельных расчетов.

===
Исп. литература для статьи «МЕЖФАЗНЫЕ СКАЧКИ ПОТЕНЦИАЛА»: Дамаскин Б. Б., Петрий О. А., Введение в электрохимическую кинетику, 2 изд., М., 1983. Б. Б. Дамаскин.

Страница «МЕЖФАЗНЫЕ СКАЧКИ ПОТЕНЦИАЛА» подготовлена по материалам химической энциклопедии.