1.7. Расчеты для систем с водородными связями
Системы с водородными связями играют важную роль в химии и биологии, поэтому для их изучения широко применяются как экспериментальные, так и теоретические методы. Квантовохимические расчеты для систем с водородными связями проводят полуэмпирическими (ППДП/2, ППДП/БУ, МЧПДП/3Н и МПДП/Н) и неэмпирическими методами. Наибольшее число работ, опубликованных за последние 20 лет, выполнено методами ППДП/2 и ОСТ-3 ГФ [63]. Однако эти методы имеют ряд существенных недостатков. Для большинства систем они в 1,5 - 2 раза переоценивают энергию образования водородных связей и на 0,02—0,03 нм занижают их длину. Кроме того, при решении прикладных задач, наряду с вычислением энергии и длины водородной связи обычно приходится рассчитывать термохимические параметры соединений и комплексов с водородными связями. Методы ППДП/2 и ОСТ-3ГФ не позволяют этого сделать, в результате область их применения при изучении реакционной способности систем с водородными связями ограничена. Ими пользовались в течение длительного времени только потому, что более точных и столь же экономичных методов не было.
Таблица 1.13. Вычисленные энергии водородных связей (кДж/моль) [64]
| Комплекс | ППДП/БУ | ППДП/2 | ОСТ-ЗГФ | 4-31ГФ | Экспсримен |
| Н2О...ОН | 184 | 302 | 294 | 172 | 142 |
| Н2О...О2Н3 | 87 | 155 | 155 | 126 | 97 |
| Н3О+...ОН2 | 113 | 252 | 250 | 185 | 136 - 155 |
В работе [64] была сделана попытка использовать для изучения реакционной способности систем с водородными связями метод ППДП/БУ. Оказалось, что по сравнению с методами ППДП/2 и ОСТ-ЗГФ он дает заметно более точные результаты при расчете энергий водородных связей. Это особенно хорошо видно на примере прочности водородных связей в заряженных системах (табл. 1.13), точность получается примерно такая же, как в неэмпирических расчетах с использованием базиса 4-31ГФ [65]. Однако метод ППДП/БУ существенно занижает длину водородных связей (немного сильнее, чем методы ППДП/2 и ОСТ-ЗГФ) и дает большие ошибки при расчете термохимических параметров органических соединений. Поэтому метод ППДП/БУ, так же как и методы ППДП/2 и ОСТ-ЗГФ, вряд ли целесообразно использовать при количественном решении прикладных задач.
Для изучения реакционной способности органических и биоорганических систем с водородными связями необходим метод, который позволял бы одновременно вычислять как термохимические параметры молекул и переходных состояний, так и параметры систем с водородными связями. В настоящее время этим требованиям удовлетворяют методы МЧПДП/3Н и МПДП/Н [66 -71], которые являются модифицированными вариантами широко известных методов МЧПДП/3 и МПДП. Основной недостаток методов МЧПДП/3 и МПДП заключается в том, что они не могут быть использованы для изучения систем с водородными связями, хотя последние очень часто встречаются при решении прикладных задач, особенно когда мы имеем дело с биоорганическими соединениями. В методах МЧПДП/3Н и МПДП/Н этот недостаток устранен за счет небольшой модификации некоторых эмпирических формул, которые используются для оценки матричных элементов. Кроме этих двух методов, для расчета параметров систем с водородными связями можно использовать метод AM1, но по точности он заметно уступает методу МПДП/Н.
Неэмпирические расчеты для систем с водородными связями в настоящее время чаще всего проводят с использованием валентно-расщепленных базисов (обычно 3-21ГФ или 4-31ГФ). Их выбор связан с необходимостью идти на компромисс между точностью расчета и затратами машинного времени. Расчеты в этих базисах немного завышают энергию образования водородных связей, занижают их длину (расстояние между гетероатомами), а также существенно переоценивают стабильность циклических структур с водородными связями. Так, при использовании базисов 3-21ГФ и 4-31ГФ циклический димер воды получается стабильнее линейного [65].
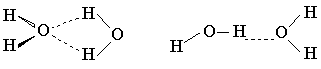
Циклическая структура комплекса аниона с водой стабильнее линейной [72]
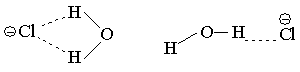
и т.д., хотя из эксперимента известно, что линейные структуры являются более стабильными. Включение в базис поляризационных орбиталей устраняет эти недостатки [73]. Таким образом, мы видим, что при использовании неэмпирических методов расчеты для систем с водородными связями желательно проводить в базисах с поляризационными орбиталями, т.е. использовать базис 6-31ГФ* или 6-31ГФ**, однако сделать это практически очень трудно, так как системы с водородными связями, которые представляют интерес для органической химии и биохимии, обычно имеют большие размеры и их свойства не удается моделировать с помощью простых систем, состоящих из небольших молекул.
В табл. 1.14 - 1.16 сопоставлены результаты квантовохимических расчетов параметров систем с водородными связями методами ППДП/2, МПДП/Н и 4-31ГФ. Из этих данных видно, что методы МПДП/Н и 4-31ГФ дают приблизительно одинаковые результаты. Следует, однако, отметить, что метод МПДП/Н в отличие от 4-31ГФ правильно передает относительную стабильность линейных и циклических систем с водородными связями. Метод ППДП/2 существенно уступает по точности методам МПДП/Н и 4-31ГФ.
Таблица 1.14. Энергии водородных связей (кДж/моль) [70]
| У—Н...Х | ППДП/2 | МПДП/ВС | 4-31ГФ | Эксперимент | |
| У—Н | X | ||||
| Н2О | Н2О* | 37 | 18 | 34 | 21 |
| Н2О | ОН - | 302 | 134 | 172 | 142 |
| Н2О | ОН- •Н2О | 155 | 88 | 126 | 97 |
| Н2O | ОН- •2Н2О | 105 | 63 | 97 | 76 |
| Н3О+ | Н2О | 252 | 130 | 185 | 137 - 155 |
| Н3О+ •Н2О | Н2О | 147 | 97 | 130 | 92 - 97 |
| Н3О+ • 2Н2О | Н2О | 105 | 80 | 109 | 71 |
| NН3 | Н2О | 19 | 8 | 15 | — |
| Н2О | NH3 | 46 | 12 | 33 | — |
| NH3 | NH3 | 19 | 4 | 14 | 19 |
| NH4+ | Н2О | — | 82 | 118 | 71 |
| NH4+•Н2О | Н2О | — | 71 | — | 63 |
| NН4+ •2Н2О | Н2О | — | 63 | — | 55 |
| NH4+• 3Н2О | Н2O | — | 47 | — | 50 |
| NH4+ | NH3 | — | 155 | 130 | 105 |
| NH4+•NH3 | NH3 | — | 97 | — | 76 |
| NH4+• 2NH3 | NH3 | — | 71 | — | 59 |
| NH4+• 3NH3 | NH3 | — | 59 | — | 50 |
| FH | Н2О | 63 | 38 | 59 | 30 |
| Н2О | FH | 13 | 21 | 21 | — |
| FH | NH3 | 84 | 50 | 63 | — |
| NH3 | FH | 6 | 9 | 13 | — |
| FH | FH* | 39 | 37 | 33 | 21 - 29 |
| FH | F - | 428 | 197 | — | 168 - 252 |
| Н2О | F -* | 334 | 130 | — | 97 |
| Н2О | F -•Н2О* | — | 97 | — | 71 |
| Н2О | F - •2Н2О* | — | 76 | — | 59 |
| Н2О | F -•ЗН2О* | — | 50 | — | 55 |
*Данные для наиболее стабильной линейной структуры.
При решении прикладных задач в случае систем с водородными связями часто возникает необходимость вычислять сечения ППЭ для реакций переноса протона между гетероатомами, так как эти процессы сопровождают многие органические и биоорганические реакции. Расчет сечения ППЭ переноса протона провести относительно легко, но при этом необходимо учитывать сильную зависимость результата от длины водородной связи. Так, в системах H2O...OH и Н2O...Н3О+ при расстояниях О...О меньше 0,25 нм на сечении ППЭ получается только один минимум, который соответствует положению протона посредине между атомами кислорода. При расстоянии О...О больше 0,25 нм на сечении ППЭ будут уже два минимума, соответствующие положению протона либо у одного атома кислорода, либо у другого. Потенциальный барьер между этими минимумами очень быстро возрастает с увеличением расстояния между атомами кислорода [64, 74, 75]. В работе [64] показано, что в ходе переноса протона расстояние O...Oможет немного уменьшиться и при этом активационный барьер переноса протона будет снижаться. Рассмотрим в качестве примера результаты расчетов методами МПДП/Н и 4-31ГФ сечения ППЭ для синхронного переноса двух протонов в циклическом димере муравьиной кислоты.
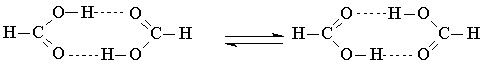
Таблица 1.15. Вычисленные расстояния (нм) между гетероатомамн (X—Y) (длины водородных связей) [70]
| У—Н...Х | ППДП/2 | МПДП/Н | 4-31ГФ | |
| У—Н | X | |||
| Н2O | Н2O | 0,254 | 0,262 | 0,283 |
| Н2O | OH - | 0,234 | 0,242 | 0,245 |
| Н3О+ | H2O | 0,234 | 0,244 | 0,236 |
| NН3 | H2O | 0,269 | 0,290 | 0,319 |
| Н2O | NН3 | 0,258 | 0,300 | 0,298 |
| NH3 | NН3 | 0,274 | 0,340 | 0,336 |
| NH4+ | Н2O | — | 0,273 | 0,265 |
| NH4+ | NH3 | — | 0,254 | 0,275 |
| HF | Н2О | 0,242 | 0,254 | 0,260 |
| Н2O | HF | 0,255 | 0,268 | 0,292 |
| HF | NH3 | 0,246 | 0,253 | 0,272 |
| NH3 | HF | 0,275 | 0,286 | 0,319 |
| HF | PA | 0,244 | 0,256 | 0,270 |
Таблица 1.16. Перенос электронной плотности с X на Y—Н при образовании водородных связей У—Н...Х (единицы заряда электрона) [70]
| У—Н...Х | ППДП/2 | МПДП/Н | 4-31 ГФ | |
| У—Н | Х | |||
| Н2O | Н2O | 0,036 | 0,007 | 0,028 |
| Н2О | NН3 | 0,059 | 0,007 | 0,037 |
| H2O | HF | — | 0,014 | 0,028 |
| HF | Н2O | 0,064 | 0,036 | 0,036 |
| HF | NН3 | 0,097 | 0,064 | 0,057 |
| H2O | OH - | 0,365 | 0,207 | 0,210 |
| H2O | ОН-•Н2O | — | 0,132 | 0,130 |
| Н2O | ОН - •2Н2O | — | 0,109 | 0,100 |
| Н3О+ | Н2O | 0,289 | 0,139 | 0,140 |
| Н3О+ •Н2O | Н2O | — | 0,086 | 0,080 |
| Н3О+•2Н2O | Н2O | — | 0,073 | 0,070 |
Из эксперимента известно, что высота активационного барьера этой реакции мала, однако в ряде опубликованных работ квантовохимические расчеты привели к противоположному результату [76 - 83] Это связано с тем, что не проводилась полная оптимизация геометрии и не учитывалось изменение длины водородных связей в переходном состоянии. Высота активационного барьера рассматриваемой реакции, вычисленная с полной оптимизацией геометрии методами МПДП/Н и 4-31ГФ, составила менее 40 кДж/моль [69, 72]. Полученные геометрические параметры приведены в табл. 1.17. Из этих данных видно, что в ходе переноса протонов в переходном состоянии происходит сжатие димера. Длина водородной связи (расстояние между атомами кислорода) уменьшается на 0,03 - 0,04 нм. За счет этого снижается высота активационного барьера. Если зафиксировать расстояние между атомами кислорода в водородных связях, то высота активационного барьера увеличится до 280 кДж/моль.
Таблица 1.17. Межатомные расстояния (нм) димера муравьиной кислоты и переходного состояния реакции синхронного переноса двух протонов [69]
| Связь | Димер | Переходное состояние | |||
| МПДП/Н | 4-31ГФ | эксперимент | МПДП/Н | 4-31ГФ | |
| С=O | 0,122 | 0,122 | 0,122 | 0,128 | 0,126 |
| С—О | 0,133 | 0,131 | 0,132 | 0,128 | 0,126 |
| O...O | 0,261 | 0,270 | 0,270 | 0,237 | 0,239 |
| С—Н | 0,110 | 0,107 | 0,108 | 0,110 | 0,107 |
Из приведенного в настоящей главе материала читатель смог убедиться, что квантовохимические расчеты позволяют получать много полезной информации о реакционной способности органических соединений, которая представляет интерес для специалистов в области тонкого органического синтеза и физической органической химии. Это прежде всего индексы реакционной способности. В некоторых случаях они дают возможность определить направление реакции, а иногда и выход конечных продуктов. Более детальную информацию о механизме реакции удается получить на основе расчетов тепловых эффектов и энергий активации.
Расчеты индексов реакционной способности обычно проводят полуэмпирическими методами (чаще всего пользуются методом ППДП/2), при этом либо используют геометрию, полученную экспериментально, либо полагают, что все межатомные расстояния и валентные углы равны своим стандартным значениям. При вычислении термодинамических параметров необходимо находить оптимальную геометрию, соответствующую минимуму полной энергии. Расчеты с оптимизацией геометрии целесообразно проводить методами МПДП или 3-21 ГФ. Эти методы позволяют вычислять геометрию как стабильных соединений, так и короткоживущих интермедиатов и переходных состоянии. Для уточнения значений термодинамических параметров иногда достаточно провести расчет с фиксированной геометрией в базисе 6-31ГФ. Для получения более надежных результатов необходимо включить в базис поляризационные орбитали на всех атомах и учесть энергию корреляции. Однако практически сделать это можно лишь для систем, содержащих небольшое число атомов. Для соединений, которые представляют интерес для органической и биоорганической химии, приходится ограничиться расчетами методом МПДП. В этом случае необходимо предварительно на небольших модельных системах, для которых доступны данные хороших неэмпирических расчетов, убедиться, что метод МПДП дает для данного класса реакций правильные результаты.


