7.3.5. Разрушение пен Механизмы разрушения пен.
В ряде случаев существует необходимость в разрушении пен, образование которых нежелательно, например, в некоторых технологических процессах текстильного или бумажного производства. Способы пеногашения, естественно, основаны на замещении или разрушении структурных адсорбционных слоев, стабилизирующих пену. Некоторые пены разрушаются низкомолекулярными спиртами, которые благодаря своей высокой поверхностной активности, как и при разрушении эмульсий, способны вытеснять стабилизатор из поверхностного слоя, но сами не дают механически устойчивых адсорбционных слоев.
Для разрушения стойких пен используют также различные механические средства, тепловое «пережигание» пленок и др.
Однако, пены значительно отличаются от концентрированных эмульсий тем, что для них важное значение имеет также диффузионный механизм разрушения, связанный с различным давлением газа в пузырьках.
Пена, как и любая дисперсная система, является агрегативно неустойчивой. Нестабильность пены объясняется наличием избытка поверхностной энергии, пропорциональной поверхности раздела фаз «жидкость–газ».
Известно, что замкнутая система, обладающая избытком внутренней энергии, находится в неустойчивом равновесии, поэтому энергия такой системы всегда уменьшается. Этот процесс протекает до момента достижения минимального значения энергии, при котором в системе наступает равновесие. Если такая система состоит из различных фаз, например, жидкости и газа, как это имеет место в пенах, то минимальное значение внутренней энергии, а значит, и поверхности раздела, будет достигнуто тогда, когда вся пена превратится в жидкость и газ.
Разрушение пены происходит в результате протекания следующих процессов:
– истечения жидкости из пенных пленок и каналов;
– диффузии газа через пленки из мелких пузырьков в крупные;
– разрыва пленок между ячейками пены.
Преобладание того или иного механизма разрушения пен зависит от многих факторов. Например, в пенах высокой кратности (сухих) истечения жидкости не происходит. Наоборот, они способны капиллярно впитывать жидкость. В таких пенах и пенах средней кратности с высокой вязкостью пленок процесс синерезиса затруднен и разрушение пен обусловлено диффузией газа через пленки. Пены низкой кратности и средней кратности с невысокой вязкостью пленок разрушаются в результате вытекания жидкой фазы из пленок, которые утончаются. Дальнейшее разрушение происходит в результате диффузии газа и разрыва пленок.
Истечение жидкости из пен.Истечение жидкости из пен происходит по каналам Плато-Гиббса под действием сил тяжести и капиллярных сил всасывания. В пенах и в вертикальных свободных пленках эти силы действуют одновременно. В горизонтальных свободных пленках влияние гравитационных сил отсутствует и процессы утончения и разрушения таких пленок происходят под действием только капиллярных сил, которые, как показано ранее, зависят от кривизны канала и центрального участка пленки.
Гравитационные силы регулируют истечение жидкости черезвсю сеть каналов Плато, но оказывают пренебрежимо малое влияние на переток жидкости из пленокк этим каналам, который обусловлен, главным образом, капиллярнымисилами и не зависит от ориентации пленки. Это подтверждает простой расчет. Если принять длину капилляра l равной 0,05 см, то максимальное давление вследствие истечения жидкости под действием гравитационных сил из пленок к каналам Плато составит 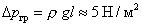 .
.
Радиус кривизны r канала Плато всегда меньше длины канала. Допустив, что r =0,5 l, получим значение давления вследствие капиллярных сил
Dpк = s / r =120 Н/м2 при s=0,03 Н/м.
Поведение жидкости в пене, находящейся в гравитационном поле, определяется соотношением между капиллярными силами и силой тяжести, выраженным в виде условия гидростатического равновесия (2.7.25).
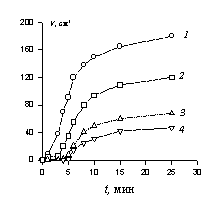 |
Концентрация ПАВ,%: 1 – 0,3; 2 – 0,5; 3 – 1;4 – 3. На первой стадии послеобразования пены преобладают капиллярные силы (rg<- дрП/дh), под действием которых происходит перетекание жидкости из пленок в каналы Плато – Гиббса. Такое перераспределение жидкойфазы внешне выражается в «задержке» истеченияжидкости, которая в работе названа периодом накопления. Этот период характеризуется интенсивным укрупнением пузырьков в результате диффузии газа и расширением каналов Плато–Гиббса. Период «задержки» включает также время, необходимое для накопления жидкости в нижнем сечении пенного столба. Продолжительность «задержи» увеличивается с ростом кратности пены и уменьшается (до критического значения) с увеличением ее столба.
Истечение жидкости начинается при условии (rg>- дрП/дh) и состоит из стадии ускорения истечения и синерезиса, протекающего с постоянной скоростью. По мере истечения жидкости возникает и возрастает градиент капиллярного давления по высоте столба, препятствующий дальнейшему вытеканию жидкости. Скорость вытекания непрерывно уменьшается вплоть до полного разрушения пены.
Типичные кривые истечения жидкости из пен, полученных методом барботирования воздуха через растворы ПАВ - сульфонола НП-1, иллюстрирует рис. 2.71. Как видно из данных этого рисунка уже при концентрации ПАВ в растворе 0,5% наблюдается некоторая задержка истечения, продолжительность которой возрастает с ростом концентрации ПАВ. Видно, что истечение жидкости происходит в три этапа: вначале скорость увеличивается до некоторого максимального значения, затем она остается некоторое время постоянной и, наконец, довольно быстро снижается. Наибольшая скоростьистечения характерна длянизких концентраций ПАВ. Времядостижения постоянной скорости истечения с ростом концентрации ПАВ увеличивается.
При наступлении стационарного потока жидкости процесс истечения описывается эмпирическим уравнением
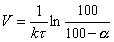 , (2.7.35)
, (2.7.35)
где V – скорость истечения жидкости;k– постоянная скорости истечения; t–время истечения;a–доля выделившейся жидкости, %.
Для теоретического и экспериментального исследования истечения жидкости из пен многие авторы используют физические модели этого явления. При этом скорость потока жидкости под действием силы тяжести определяют по уравнению Пуазейля:
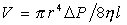 , (2.7.36)
, (2.7.36)
где r и l – радиус и длина капилляра в пене в момент времени t; DP- разность давлений на концах капилляра;h – вязкость жидкости.
Уравнение Пуазейля справедливо для истечения жидкостей из цилиндрического капилляра, а так как жидкость в пене течет в канале треугольного сечения, то его применение к пенам предполагает определенные допущения.
Если пенурассматривать как группу капилляров, в которой течение жидкости подчиняется уравнению (2.7.36), можно получить следующее выражение, описывающее кинетику истечения жидкости из пены:
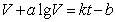 , (2.7.37)
, (2.7.37)
где V – объем жидкости, вытекшей за время t; a, b и k– постоянные.
Это уравнение справедливо для истечения жидкости практически на протяжении всего процесса, за исключением начального и конечного периодов. Значения постоянных k, а и b зависят от природы и концентрации ПАВ в растворе. Однако, интерпретация физического смысла этих постоянных затруднительна, вследствие чего уравнение имеет ограниченное применение.
Диффузионный механизм разрушения пен.Наряду со слиянием пузырьков воздуха или газа в результате разрыва жидких пленок в пене возможен рост более крупных пузырьков за счет мелких, так как в последних большее давление растворения газа, зависящее от кривизны поверхности раздела фаз. Для пен этот процесс имеет существенное значение, особенно если пленки пен очень устойчивы вследствие большой вязкости образующей их жидкости.
Несмотря на высокую устойчивость, эти пены с течением времени изменяется таким образом, что более мелкие пузырьки уменьшаются и исчезают, а более крупные увеличиваются. Этот процесс объясняется диффузией газа из мелких пузырьков в более крупные.
Свободную газовую фазу над пеной (атмосферу) можно рассматривать как один бесконечно большой пузырь, в который постепенно переходит диспергированный газ, благодаря чему столб пены уменьшается.
Причиной подобного перехода газа является разность давлений в различных по величине ячейках пены. Если пузырьки в первом приближении считать сферическими, то повышение давления в них по сравнению с внешней газовой фазой можно описать уравнением Лапласа
P = 2s / r, (2.7.38)
где s – поверхностное натяжение жидкости (раствора ПАВ), r- радиус пузырька.
Разность давления газа в двух пузырьках с различными радиусами r1 и r2 выражается как
DP = 2s (1/r1 – 1/r2), (2.7.39)
где r1 < r2.
Диффузионный поток газа через пленку можно описать с помощью первого закона Фика
dn / dt = - DА dс/ dx, (2.7.40)
где D – коэффициент диффузии; А – площадь слоя, через который проходит диффузия; dс/dx – градиент концентрации растворимого газа в пленке, разделяющей оба пузырька.
Количество газа (n молей), выходящего из маленького пузырька за единицу времени (t), будет
dn /dt = -4p r2 D dс/dx. (2.7.41)
Градиент концентрации dс/dx в стационарном процессе диффузии можем считать примерно равным Dс / l, где Dс – разность концентраций газа у поверхностей раздела пленки с маленьким и большим пузырьками, а l – средняя толщина жидкой прослойки между ними.
Разность концентраций можно выразить через разность давлений при помощи закона Генри:
Dс = a DP,
где a – коэффициент поглощения газа жидкостью.
Рассматривая случай сильно полидисперсной пены, когда r1 << r2, можно упростить уравнение (2.7.39):
DP = 2 s (1/r1 – 1/r2) ≈ 2 s/r1 . (2.7.42)
Из уравнения (2.7.41) с учетом того, что dс/dx ≈ Dс/ l, можем записать уравнение для диффузии:
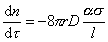 . (2.7.43)
. (2.7.43)
Полагая, что для газа в пузырьках применимо уравнение состояния идеального газа
PV = n RT,
записывая для n молей n = PV/RT и учитывая, что объем сферического пузырька
V= (4/3) pr3,
а избыточное давление в пузырьке
Р = Р0 + 2 s / r,
где Р0 – внешнее давление, можем записать
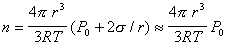 , (2.7.44)
, (2.7.44)
так как величина 2 s/rобычно мала по сравнению с внешним давлением Р0.
После подстановки выражения для n в уравнение (2.7.43) и его интегрирования получаем
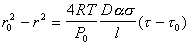 , (2.7.45)
, (2.7.45)
где r0 – радиус пузырька в начальный момент времени t0.
Из уравнения (2.7.45) следует, что радиус пузырька уменьшается пропорционально корню квадратному времени. Эта зависимость была проверена Де Фризом в 1957 г.,проводившим фотографирование пены очень вязких веществ через различные промежутки времени.
Разрушение пленок.Пленка пены при достижении определенной (критической) толщины разрушается. Это третий важный фактор разрушения пен в процессе их старения. Механизм разрушения толстых и тонких черных пленок не одинаков. Это - обусловлено тем, что благодаря наличию прослойки раствора между адсорбционными слоями обе поверхности толстой пленки могут рассматриваться независимо.
Согласно теории разрыва толстых пленок Де Фриза разрушение происходит вследствие образования отверстия критического размера. Возникновение этого отверстия (которое имеет флуктуационное происхождение) сопровождается уменьшением поверхностной энергии, поскольку, по крайней мере в начальный момент, поверхность раздела при разрыве пленки увеличивается.
Прирост общей поверхности разрушающейся пленки толщиной d можно вычислить по уравнению де Фриза
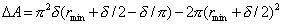 , (2.7.46)
, (2.7.46)
гдеrmin – минимальный радиус отверстия в пленке.
Максимальное увеличение поверхности раздела DAmax достигается при
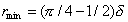 .
.
Подставляя это выражение в (2.7.46), получаем:
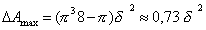 . (2.7.47)
. (2.7.47)
Максимальное увеличение свободной поверхностной энергии при расширении отверстия составляет
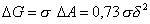 . (2.7.48)
. (2.7.48)
Из уравнения (2.7.48) следует, что процесс разрушения в большей степени зависит от толщины пленки, чем от поверхностного натяжения. Поэтому вероятность разрыва больше для пленок меньшей толщины. Энергия активации при d = 15 нм и s =30÷40 мДж/м2 составляет » 5∙10-18 Дж. Пленки из чистой жидкости могут иметь значительно меньшую толщину, соизмеримую с размером молекул, поэтому предотвратить самопроизвольное разрушение таких пленок невозможно.
В соответствии с представлениями известного болгарского ученого А. Шелудко разрыв пленки обусловлен образованием на поверхностях пленки искривленных участков. Они возникают под действием тепловых флуктуаций и приводят к локальным изменениям толщины пленки. На утолщенный участок пленки действуют возникающие в нем местное капиллярное давление DPк и отрицательное расклинивающее давление П с направлением, противоположным капиллярному, которое восстанавливает толщину пленки. Если нарастающее расклинивающее давление по абсолютной величине превышает капиллярное давление, локальный прогиб пленки увеличивается, и она разрушается. Из условия разрыва пленки dП/ dd = dDPк/ dd было получено уравнение для ее критической толщины:
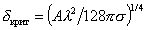 . (2.7.49)
. (2.7.49)
Это уравнение справедливо при следующих допущениях: Dd<
Уравнение (2.7.49) не учитывает влияния электростатической составляющей расклинивающего давления, поэтому оно справедливо только для нестабильных пленок. Кроме того, оно содержит величину l, данные о которой еще отсутствуют. Однако имеются основания полагать, что длина волны прогиба поверхности пленки пропорциональна ее радиусу. Образование волн на поверхности пленки вследствие теплового движения наблюдают при изучении рассеяния света пленками.
Согласно теории А. Шелудко для разрыва пленки не обязательно достижение критической толщины dкрит. Если существует устойчивая толщина d< dкpит, то в пленке должны образовываться тонкие места в виде «черных пятен» с толщиной d. В достаточно толстой пленке истечение жидкости происходит обычно быстрее, чем в тонкой, а рост флуктуаций – медленнее или его нет вообще. Однако, когда пленка становится тонкой, скорость истечения жидкости уменьшается, а флуктуации, если они есть, быстро растут до тех пор, пока толщина пленки не достигнет критического значения. Экспериментальная проверка этой теории показала, что утончение происходит быстрее, чем предсказывает теория, а критическая толщина пленки несколько меньше теоретического значения, по-видимому, вследствие неровности ее поверхности.
Постепенное утончение пленки происходит в результате истечения из нее жидкости под влиянием гравитационных сил и сил всасывания в каналы Плато. Пленки толщиной »0,1мкмутончаются в результате взаимного влияния ван-дер-ваальсовых сил притяжения и сил отталкивания, возникающих в двойном электрическом слое. При дальнейшем утончении некоторые пленки становятся метастабильными, другие - разрушаются при достижении толщины 0,05-0,01 мкм. Метастабильность пленок проявляется при взаимном уравновешивании сил всасывания в каналы Плато, сил притяжения и электростатических сил отталкивания. Нестабильность пленок пен является следствием преобладания сил притяжения.
При разрушении пленки в ее центральной части образуется круглое отверстие. В результате расширения этого отверстия перед краями фронта распространяется в виде окружности с увеличивающимся радиусом «ореол», представляющий собой утолщенную область пленки. Фронт волны фактически распространяется со скоростью, уменьшающейся в направлении от отверстия. Разрыв пленки сопровождается образованием капель, направление и скорость движения которых соответствуют параметрам фронта распространяющейся волны. Средний радиус капель, образующихся при разрыве пленки, практически не зависит от ее толщины и в интервале толщины пленки 0,58-1,16мкм составляет 40-55 мкм.
Разрыв пленок пузырьков на водной поверхности имеет большое значение в природе и практической деятельности человека. Так, из капель, образующихся при разрыве пузырьков на поверхности океана, в результате испарения воды возникают ядра конденсации, на которых конденсируется атмосферная влага (образование облаков). В результате разрушения пленок пузырьков на водной поверхности очистных сооружений содержащиеся в стоках микроорганизмы попадают в воздушную среду и распространяются на значительные расстояния от источника загрязнения.
Разрушение пузырьков в столбе пены происходит после того, как закончатся процессы истечения и диффузии, а пленки пены достигнут критической толщины. Вид распада определяется структурой пены и свойствами ПАВ. Уменьшение высоты столба пены связано с разрывом поверхностных пленок и изменяется во времени по логарифмическому закону:
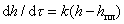 , (2.7.50)
, (2.7.50)
где h– высота столба пены в момент времени t, hпл – высота столба выделившейся междупленочной жидкости; k – постоянная скорости распада.
При интегрировании уравнения(2.7.50) получаем
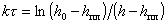 , (2.7.51)
, (2.7.51)
гдеh0 – начальная высота столба пены.
Если заменить высоту столба пены и жидкости их объемами и пренебречь объемом жидкости в пене, получаем
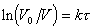 . (2.7.52)
. (2.7.52)
Можно отметить, что разрушение пены формально описывается уравнением первого порядка.


