1.5. Поверхностное натяжение растворов и адсорбция
Свободная поверхностная энергия самопроизвольно может только уменьшаться, что проявляется в уменьшении либо поверхности раздела фаз, либо межфазного (поверхностного) натяжения. Поверхностное натяжение может уменьшаться в результате самопроизвольного перераспределения компонентов системы между объемами фаз a и b и поверхностью их раздела. В поверхности раздела фаз будут преимущественно концентрироваться те компоненты, которые способны уменьшать избыточную свободную поверхностную энергию. Это явление получило название «адсорбция». Количественно мерой адсорбции служит избыток вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же слое в объеме фазы. Этот избыток обычно относят к единице площади поверхности (или к единице массы адсорбента). Такая адсорбция называется гиббсовской и обозначается буквой Гi. Поверхностный избыток является алгебраической величиной. Если он положителен, то вблизи поверхности данный компонент присутствует в избытке, если отрицателен, то концентрация компонента на поверхности фазы ниже, чем в ее объеме .
Рассмотрим распределение в системе i -го компонента, предполагая, что это вещество способно понижать поверхностное натяжение. В соответствии с уравнением (1.1.6) число молей n вещества i-го компонента в системе определяется как 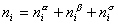 .
.
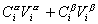 . (1.1.81)
. (1.1.81)
где Сa, Сb- концентрация вещества в фазах a, b.
Количество вещества на поверхности раздела фаз 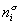 , избыточное по отношению к объемам фаз Va и Vb, оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны,
, избыточное по отношению к объемам фаз Va и Vb, оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны, 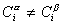 .
.
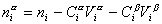 . (1.1.82)
. (1.1.82)
Разделив выражение (1.1.82) на площадь поверхности раздела фаз А, можем определить гиббсовскую адсорбцию:
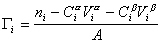 . (1.1.83)
. (1.1.83)
Фундаментальным уравнением физической химии поверхностей является взаимосвязь между адсорбцией и межфазным натяжением, которую можно определить экспериментально при одновременном изменении многих факторов. Остановимся на системах, в которых адсорбция протекает при постоянной температуре. Связь между адсорбцией и межфазным натяжением при постоянной температуре T называется изотермой адсорбции, фундаментальное уравнение которой известно как уравнение Гиббса. Рассмотрим его вывод.
При небольшом обратимом изменении энергии системы dU с учетом формулы (1.1.4) можем написать
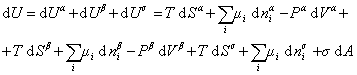 , (1.1.84)
, (1.1.84)
где U – полная внутренняя энергия системы; Ua, Ub, Us– внутренняя энергия фаз aиb и поверхности их раздела; Pa, Pb - давление в фазах aиb; m - химический потенциалi-того компонента; Sa, Sb, Ss – энтропия фаз a иb и их поверхности раздела; s - поверхностное натяжение.
Поскольку из курса химической термодинамики известно, что
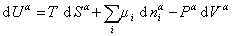 (1.1.85)
(1.1.85)
и
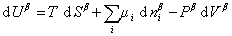 , (1.1.86)
, (1.1.86)
то
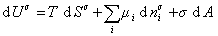 . (1.1.87)
. (1.1.87)
Если энергию, энтропию и количество компонентов увеличивать от нуля до некоторого определенного значения при постоянстве температуры T, площади поверхности раздела фаз A и количестве вещества на этой поверхности 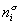 , то уравнение (1.1.87) переходит в общее уравнение
, то уравнение (1.1.87) переходит в общее уравнение
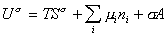 , (1.1.88)
, (1.1.88)
дифференцирование которого приводит к выражению
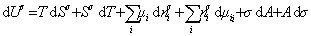 . (1.1.89)
. (1.1.89)

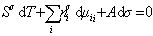 . (1.1.90)
. (1.1.90)
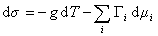 , (1.1.91)
, (1.1.91)
где 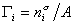 – гиббсовская адсорбция;
– гиббсовская адсорбция; 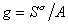 – удельная энтропия поверхностного слоя.
– удельная энтропия поверхностного слоя.
При постоянной температуре
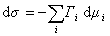 . (1.1.92)
. (1.1.92)
Для двухкомпонентной системы
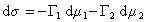 , (1.1.93)
, (1.1.93)
где индекс 1 относится к растворителю, а индекс 2 – к растворенному веществу.
|
Разделяющая поверхность Гиббса может быть проведена так, чтобы обратилась в нуль адсорбция любого наперед заданного компонента, но только одного, как это показано на рис. 1.15.
Расстояние между двумя плоскостями (разделяющими поверхностями), одна из которых соответствует условию Гj = 0, а другая - Гk = 0, обозначим dkj:
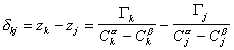 , (1.1.94)
, (1.1.94)
где Гk, Гj– избытки  рассматриваемых компонентов в поверхностном слое ; Cka, Ckb, Cja, Cjb – концентрация компонентов k и j в фазах a и b; zk, zj – координаты разделяющей поверхности.
рассматриваемых компонентов в поверхностном слое ; Cka, Ckb, Cja, Cjb – концентрация компонентов k и j в фазах a и b; zk, zj – координаты разделяющей поверхности.
Поскольку значения Г1 в уравнении (1.1.93) определены относительно произвольно выбранного положения разделяющей плоскости, то ее можно расположить так, чтобы избыток растворителя в поверхностном слое был равен нулю ( Г1 = 0).
Тогда
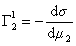 , (1.1.95)
, (1.1.95)
где верхний индекс 1 означает, что для выбранной поверхности раздела Г1=0.
Учитывая зависимость химического потенциала от активности растворенного вещества
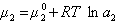 , (1.1.96)
, (1.1.96)
получаем после дифференцирования уравнения (1.1.96)
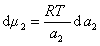 , (1.1.97)
, (1.1.97)
где 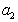 - активность растворенного вещества.
- активность растворенного вещества.
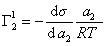 . (1.1.98)
. (1.1.98)
Из уравнения (1.1.98) следует, что если 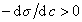 , то адсорбция положительна, а при
, то адсорбция положительна, а при 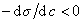 возникает дефицит растворенного вещества на разделяющей поверхности .
возникает дефицит растворенного вещества на разделяющей поверхности .
Поскольку 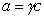 , где g – коэффициент активности, который для разбавленных растворов стремится к единице, то
, где g – коэффициент активности, который для разбавленных растворов стремится к единице, то 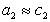 и
и
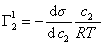 . (1.1.99)
. (1.1.99)
Уравнение (1.1.99) представляет собой наиболее употребляемую форму изотермы адсорбции Гиббса, причем так как рассматривается адсорбция именно растворенного вещества, индексы при адсорбции и концентрации опускают, т.е.
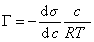 . (1.1.100)
. (1.1.100)
Исследования показывают, что существуют такие вещества, растворение которых приводит к резкому снижению поверхностного натяжения раствора. Эти вещества называют поверхностно-активными. В соответствии с уравнением Гиббса адсорбция их всегда положительна, т.е. концентрация в поверхностном слое выше объемной концентрации. По предложению Ребиндера мера поверхностной активности обозначается первой буквой фамилии Гиббса. Обычно используют значения поверхностной активности в бесконечно разбавленных растворах
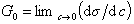 . (1.1.101)
. (1.1.101)
К классу поверхностно-активных веществ (ПАВ) относятся жирные кислоты и их соли (мыла), сульфокислоты, их соли, спирты, алкилсульфоэфиры и др. Если 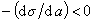 , то Г< 0 (адсорбция отрицательна). Поверхностное натяжение растворов этих веществ на границе с воздухом выше, чем на границе с чистым растворителем (водой). Такие вещества называют поверхностно-инактивными. К ним относятся минеральные соли, основания, кислоты и низшие органические кислоты.
, то Г< 0 (адсорбция отрицательна). Поверхностное натяжение растворов этих веществ на границе с воздухом выше, чем на границе с чистым растворителем (водой). Такие вещества называют поверхностно-инактивными. К ним относятся минеральные соли, основания, кислоты и низшие органические кислоты.
Очевидно, что если 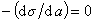 , то Г= 0 (адсорбция не происходит). Такое вещество называют поверхностно-инертным. Вещество, поверхностно-активное на одной границе раздела фаз, может быть неактивным на другой и наоборот. Приведенное выше деление веществ с соответствующими параметрами справедливо для границы водный раствор - воздух. На других границах данные вещества могут вести себя иначе.
, то Г= 0 (адсорбция не происходит). Такое вещество называют поверхностно-инертным. Вещество, поверхностно-активное на одной границе раздела фаз, может быть неактивным на другой и наоборот. Приведенное выше деление веществ с соответствующими параметрами справедливо для границы водный раствор - воздух. На других границах данные вещества могут вести себя иначе.
В 1978 г. Дюкло и Траубе сформулировали эмпирическое правило: в гомологическом ряду поверхностно-активных веществ поверхностная активность и адсорбция возрастают при переходе к каждому последующему члену гомологического ряда примерно в 3,2 раза. Однако это правило справедливо только для весьма разбавленных растворов и исключает три первых члена гомологического ряда. Математически это правило может быть записано
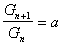 или
или 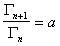 , (1.1.102)
, (1.1.102)
где n – число атомов углерода в углеводородной цепочке;
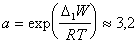 . (1.1.103)
. (1.1.103)
Зависимость поверхностной активности от числа метиленовых групп в углеводородной цепочке ПАВ выражается уравнением
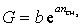 или
или 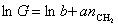 , (1.1.104)
, (1.1.104)
где 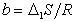 ;
; 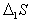 , D1W- изменение энтропии и работа переноса одного моля метиленовых групп из раствора на поверхность.
, D1W- изменение энтропии и работа переноса одного моля метиленовых групп из раствора на поверхность.
Свободно от недостатков правила Дюкло - Траубе эмпирическое уравнение Шишковского (1909 г.), устанавливающее зависимость поверхностного натяжения раствора от его концентрации:
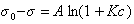 , (1.1.105)
, (1.1.105)
где А – постоянная для всего гомологического ряда, не зависящая от природы ПАВ; при температуре 20°С 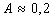 ; K – постоянная, характеризующая увеличение поверхностной активности при переходе к каждому последующему члену гомологического ряда;
; K – постоянная, характеризующая увеличение поверхностной активности при переходе к каждому последующему члену гомологического ряда; 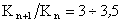 .
.
Замечательно, что это уравнение, полученное на основании обобщения экспериментальных данных, оказалось очень точным и применимым практически для всех ПАВ в широкой области концентраций растворов. Если концентрация ПАВ достаточно велика и следовательно Kc>>1, то единицей в уравнении Шишковского (1.1.105 ) можно пренебречь, тогда
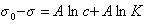
или
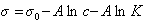 . (1.1.106)
. (1.1.106)
Обозначим постоянной В постоянные при изотермических условиях величины 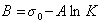 , тогда
, тогда
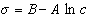 . (1.1.107)
. (1.1.107)
Следовательно, при относительно высокой концентрации растворов ПАВ их поверхностное натяжение должно уменьшаться экспоненциально с увеличением концентрации.
Уравнение (1.1.107) может быть получено непосредственно из уравнения изотермы адсорбции Гиббса:
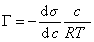 .
.
При достаточно высокой концентрации растворенного вещества адсорбция достигает предела , т.е. Г = Гmax , поэтому
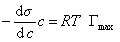 , (1.1.108)
, (1.1.108)
где при постоянной температуре правая часть представляет собой постоянную величину и может быть обозначена RT Гmax = A. Следовательно,
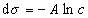 ,
,
откуда после интегрирования получаем
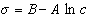 . (1.1.109)
. (1.1.109)
Таким образом, уравнение Шишковского может быть выведено из уравнения Гиббса, так как уравнения (1.1.107) и (1.1.109) идентичны. Точность уравнения Шишковского связана с тем, что в нем уже заложено условие насыщения адсорбционного слоя.
Если уравнение Шишковского в форме
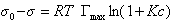 (1.1.110)
(1.1.110)
продифференцировать
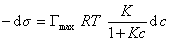 , (1.1.111)
, (1.1.111)
и подставить в уравнение Гиббса величину
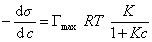 , (1.1.112)
, (1.1.112)
то уравнение изотермы адсорбции примет вид
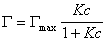 . (1.1.113)
. (1.1.113)
В такой форме уравнение изотермы адсорбции носит название изотермы Ленгмюра. Американский ученый И. Ленгмюр в 1917 г. развил представление о мономолекулярной адсорбции и на основании молекулярно- кинетической теории получил уравнение (1.1.113) .
Уравнение Шишковского позволяет определить предел адсорбции (при Kc>>1), так как в таком случае это уравнение принимает вид
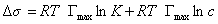 . (1.1.114)
. (1.1.114)
|
Построив график 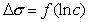 , как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.
, как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.
Понимание адсорбционных процессов имеет чрезвычайно важное значение, так как они лежат в основе многих процессов, протекающих на границе раздела фаз, например крашения, отмывания загрязнений, отделки текстильных материалов и т.д., т.е. в основе всех коллоидно -химических процессов на границе жидкость–газ.

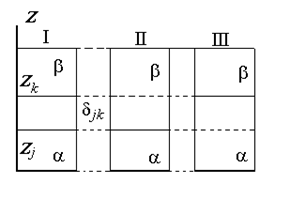 Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)
Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)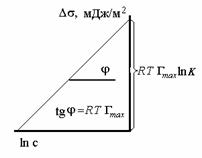 Рис. 1.16. Зависимость поверхностного натяжения от концентрации растворов ПАВ в координатах уравнения Шишковского
Рис. 1.16. Зависимость поверхностного натяжения от концентрации растворов ПАВ в координатах уравнения Шишковского
