Вудворда-Хофмана правила

ВУДВОРДА-ХОФМАНА ПРАВИЛА, предсказывают стереохим. направление и предпочтительные условия согласованных перициклич. р-ций, т.е. р-ций, протекающих без участия промежут. продуктов (см. Перициклические реакции). Для них справедлив сформулированный Р. Вудвордом и Р. Хофманом принцип сохранения орбитальной симметрии: согласованные р-ции, в к-рых заполненные молекулярные орбитали исходных реагентов и продуктов полностью соответствуют друг другу по св-вам симметрии (коррелируют между собой), протекают легче, чем р-ции, в к-рых указанное соответствие нарушается. Конкретизация этого принципа приводит к Вудворда - Хофмана правилам.

Применение Вудворда - Хофмана правил основано на выделении в реагентах и продуктах перициклич. р-ций орбиталей тех связей и групп, к-рые непосредственно включены в процессы разрыва старых и образования новых связей и образуют в переходном состоянии циклич. систему. Для описания стереохимии р-ции вводится дополнит. характеристика. Процесс, в к-ром одновременно образуются (или разрываются) связи с одной стороны плоскости молекулы, наз. супраповерхностным (обозначается s). Если эти связи в переходном состоянии расположены по разные стороны плоскости молекулы, р-цию относят к антараповерхностному типу (а). Напр., циклодимеризация этилена через переходное состояние с взаимно перпендикулярным расположением реагирующих молекул относится к s,a-присоединению:

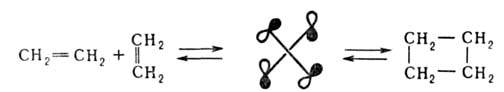
Также м. б. классифицированы электроциклич. р-ции и сигматропные перегруппировки. Напр., электроциклич. замыкание производных 1,3-бутадиена в циклобутены, осуществляющееся в условиях термич. превращения конротаторным путем (т.е. вращением концевых групп в одну сторону), описывается как s,а-циклоприсоединение: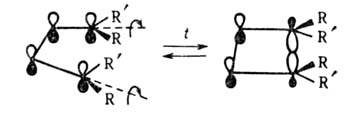

Аналогичное превращение, реализуемое фотохимически через возбужденное состояние и идущее в этих условиях дисротаторным способом (т.е. вращением концевых групп в противоположные стороны), соответствует s,s-циклоприсоединению: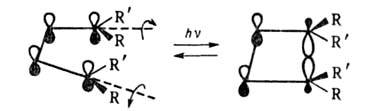

В случае 1,2-сигматропного смещения алкильной группы в карбкатионе RR'R"ССН₂СН₂⁺ перегруппировке с сохранением конфигурации мигрирующего центра соответствует s,s-циклоприсоединение, процессу с обращением конфигурации - s,a-циклоприсоединение: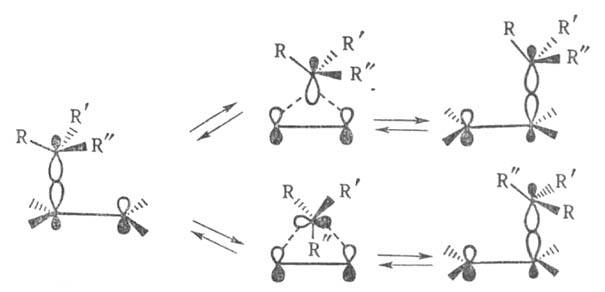

Осн. метод теоретич. анализа перициклич. р-ций-построение корреляц. диаграмм, при помощи к-рых устанавливаются соответствия по симметрии между орбиталями исходных реагентов и продуктов. Путь сближения реагентов (или отдельных связей для случая внутримол. превращения) определяет симметрию переходного состояния, в рамках к-рой устанавливаются корреляции между орбиталями реагентов и продуктов. В р-циях, разрешенных принципом сохранения орбитальной симметрии, все заполненные орбитали реагентов трансформируются в заполненные орбитали продуктов. Невыполнение этого условия -корреляция с антисвязывающими (т.е. энергетически невыгодными) орбиталями продуктов - означает симметрийный запрет р-ции в данном электронном состоянии.

Пример корреляц. диаграмм приведен на рис. Орбитали реагентов и продуктов классифицируются как симметричные S и антисимметричные А по отношению к элементам симметрии, сохраняющимся в ходе р-ции. Таковыми являются проходящие через центр связи С₂—С₃ ось симметрии второго порядка для конротаторного пути и плоскость симметрии для дисротаторного. Корреляц. линии, связывающие орбитали, показывают, что требования сохранения орбитальной симметрии выполняются для осн. состояния только в случае кон ротаторного процесса. Для дисротаторного орбиталь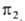1,3-бутадиена переходит в антисвязывающую орбиталь 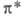циклобутена. Последняя м. б. заселена электронами только в возбужденном состоянии, поэтому дисротаторная р-ция разрешена только в возбужденном состоянии и реализуется фотохимически. Указанные предсказания полностью соответствуют эксперим. данным для разл. производных 1,3-бутадиена и циклобутена.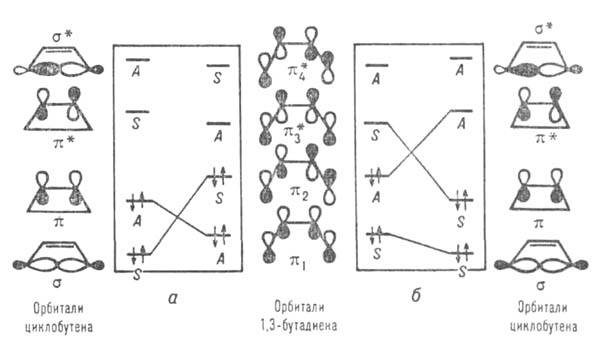

Рис. Корреляционная диаграмма превращения 1,3-бутадиена в циклобутен; а-конротаторный путь, б-дисротаторный путь.

Анализ корреляц. диаграмм разл. типов перициклич. р-ций позволил сформулировать Вудворда - Хофмана правила, определяющие возможность процесса в зависимости от общего числа электронов во взаимодействующих орбиталях и стереохимии сближения. В табл. 1-3 суммированы Вудворда - Хофмана правила для ци-клоприсоединения, электроциклич. и сигматропных р-ций соответственно.

Табл. 1. - РАЗРЕШЕННЫЕ ПО ОРБИТАЛЬНОЙ СИММЕТРИИ РЕАКЦИИ ЦИКЛОПРИСОЕДИНЕНИЯ В ЗАВИСИМОСТИ ОТ ОБЩЕГО ЧИСЛА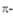ЭЛЕКТРОНОВ

Табл. 2. - РАЗРЕШЕННЫЕ ПО ОРБИТАЛЬНОЙ СИММЕТРИИ ЭЛЕКТРОЦИКЛИЧЕСКИЕ РЕАКЦИИ В ЗАВИСИМОСТИ ОТ ОБЩЕГО ЧИСЛА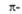 ЭЛЕКТРОНОВ

Табл. 3. - ПРАВИЛА ВУДВОРДА-ХОФМАНА ДЛЯ СИГМАТРОПНЫХ МИГРАЦИЙ АЛКИЛЬНЫХ И ИЗОЭЛЕКТРОННЫХ ИМ ГРУПП

В случае димеризации этилена общее число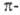электронов равно 4 (система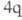,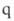=1). Следовательно (см. табл. 1), для этой р-ции s,s-присоединение должно реализоваться фотохимически, что и наблюдается экспериментально. Для s,s-присоединения 1,3-бутадиена и этилена (диеновый синтез) число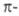электронов равно 6 (система 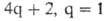) и, следовательно, предпочтительно термич. превращение.

Для всех видов перициклич. р-ций справедливо обобщенное Вудворда - Хофмана правило: в основном электронном состоянии разрешены по симметрии р-ции, для к-рых общее число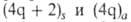 компонент нечетное. Для разрешенных по симметрии фотохим. р-ций указанное число - четное. Напр., для конротаторного s,а-замыкания 1,3-бутадиена имеется одна компонента 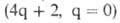и р-ция относится к типу термически разрешенных.

Принцип орбитальной симметрии не имеет исключений, однако Вудворда - Хофмана правила не являются абсолютными, и ряд р-ций, запрещенных по симметрии, практически вполне реализуем. Однако в этом случае они почти всегда осуществляются как постадийные, т.е. несогласованные процессы.

Кроме Вудворда - Хофмана правил существуют другие подходы к теоретич. анализу перициклич. р-ций, напр. граничных орбиталеп теория. Как и Вудворда - Хофмана правила, они основаны на анализе топологии (узловых характеристик) циклич. системы взаимодействующих орбиталей реагентов в переходном состоянии.

===
Исп. литература для статьи «ВУДВОРДА-ХОФМАНА ПРАВИЛА»: Вудворд Р., Хоффман Р., Сохранение орбитальной симметрии, пер. с англ., М., 1971;Минкин В. И., Симкин Б. Я., Миняев Р. М., Теория строения молекул, Электронные оболочки, М., 1979. В. И. Минкин.

Страница «ВУДВОРДА-ХОФМАНА ПРАВИЛА» подготовлена по материалам химической энциклопедии.